题目内容
【题目】已知如图等腰
，
，
，
于点
.点
是
延长线上一点，
点是线段
上一点，
，下面的结论：①
平分
；②
；③
是等边三角形；④
.其中正确的序号是________.
【答案】①③④
【解析】
①利用等边对等角，即可证得；
②因为点O是线段AD上一点，所以BO不一定是
的角平分线，可作判断；
③证明
且OP=OC，即可证得
是等边三角形；
④首先证明
,则AO=CE，AC=AE+CE=AO+AP；
∵
，
，
∴AD平分
∴
∴
平分
①正确；
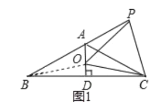
如图1，连接BO，∵AD垂直平分BC
∴OB=OC 又∵OC=OP
∴OB=OC=OP
∴
∵点O在线段AD上，∴
与
不一定相等，
则
与
不一定相等，故②不正确；
∵
∴
∵
∴
∴
又∵OP=OC
∴是等边三角形，故③正确；
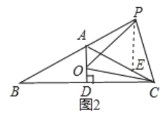
如图2，在AC上截取AE=PA，连接PB，
∵
∴
是等边三角形
∴
∴
∵
∴
∵OP=CP
∴
∴AO=CE
∴AC=AE+CE=AO+AP,故④正确；
本题正确的结论有：①③④
故答案为：①③④
【题目】某公司对一款新高压锅进行测试，放入足量的水和设定某一模式后，在容积不变的情况下，根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小．压强在加热前是100kpa，达到最大值后高压锅停止加热。为方便分析，测试员记y=p-100，
表示压强在测试过程中相对于100kpa的增加值．部分数据如下表：
温度f(℃) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | |
压强增加值 Y(kpa) | 0 | 9.5 | 18 | 25.5 | 32 | 37.5 | 42 |
（1）根据表中的数据，在给出的坐标系中画出相应的点(坐标系已画在答卷上)；
（2）y与t之问是否存在函数关系?若是，请求出函数关系式；否则请说明理由；
（3）①在该模式下，压强P的最大值是多少?
②当t分别为，t1，t2(t1<t2)时，对应y的值分别为y1 ，y2 ， 请比较
与
的大小，并解释比较结果的实际意义．
【题目】小华根据学习函数的经验，对函数
的图象与性质进行了研究，下面是小华的研究过程，请补充完成.
（1）自变量
的取值范围是全体实数，与
的几组对应值列表如下：
|
|
|
|
|
|
| 4 | 5 |
|
|
| m | 2 | 1 | 0 | n | 2 | 3 |
|
其中，m= ,n= ；
（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出该函数的图象；
（3）观察图象，写出该函数的两条性质；
（4）进一步研究函数图象发现：
①方程
有 个实数根；
②不等式
的解集为 .
