题目内容
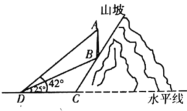
【题目】如图，为加快
网络建设，某移动通信公司在一个坡度为2∶1的山腰上建了一座垂直于水平面的信号通信塔
，在距山脚
处水平距离39米的点
处测得通信塔底
处的仰角是25°，通信塔顶
处的仰角是42°．请求出通信塔的大约高度（结果保留整数，参考数据：
，
，
，
）．
【答案】通信塔AB的大约高度为21米．
【解析】
延长AB交DC延长线于点E，根据坡度的概念设CE＝x，得到BE＝2x，根据正切的概念列式求出x，得到DE的长，根据正切的定义求出AE，计算即可．
延长AB交DC延长线于点E，则AE⊥DC.
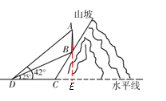
由题意知∠BDC＝25°、∠ADE＝42°、CD＝39米，
∵BC的坡度为2：1
∴设CE＝x、则BE＝2x、DE＝39+x，
在Rt△BDE中，由tan∠BDE＝
可得
≈0.5，
解得：x＝13，
∴DE＝39+x＝52、BE＝2x＝26，
在Rt△ADE中，AE＝DE·tan∠ADE≈52×0.9＝46.8，
则AB＝AE﹣BE＝46.8﹣26=20.8≈21（米），
答：通信塔AB的大约高度为21米．
小学教材全测系列答案
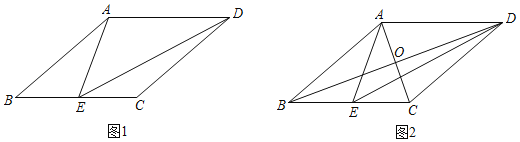
【题目】如图，∠MAN=30°，在射线AN上取一点B，使AB=4 cm，过点B作BC⊥AM于点C，点D为边AB上的动点（点D不与点A，点B重合），连接CD，过点D作ED⊥CD交直线AC于点E．在点D由点A到点B运动过程中，设AD=x cm，AE=y cm．
（1）取指定点作图，根据下面表格预填结果，先通过作图确定AD=2 cm时，点E的位置，测量AE的长度．
①根据题意，在答题卡上补全图形；
②把表格补充完整：通过取点、画图、测量，得到了x与y的几组对应值，如表：
x/cm | … |
| 1 |
| 2 |
| 3 |
| … |
y cm | … | 0.4 | 0.8 | 1.0 | m | 1.0 | 0 | 4.0 | … |
则m=______（结果保留一位小数）．
（2）在下面的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：当AE=
AD时，AD的长度约为______cm．
