题目内容
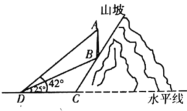
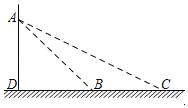
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6.2m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=45°,∠ACD=28°.求电子警察安装在悬臂灯杆上的高度AD的长.(结果精确到0.1米)(参考数据:sin28°=0.47,cos28°=0.88,tan28°=0.53)
【答案】7.0m
【解析】
首先求出DA=DB,然后在Rt△ADC中,根据正切的定义列出等量关系,求出AD的值即可.
解:根据题意可知,∠ADC=90°,
∵∠ABD=45°,
∴DA=DB,
在Rt△ADC中,∠ACD=28°,BC=6.2m,
∴tan28°=![]() ,
,
∴AD=0.53(AD+6.2),
∴AD=6.99≈7.0m,
答:电子警察安装在悬臂灯杆上的高度AD的长为7.0m.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?