Question

【题目】如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．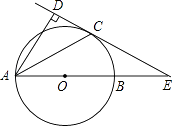

（1）求证：直线CD为⊙O的切线；
（2）当AB=2BE，且CE= 时，求AD的长．

Answer 1

【答案】
（1）证明：如图，连接OC，

∵AC平分∠DAB，

∴∠DAC=∠CAB，

∵OA=OC，

∴∠OCA=∠CAB，

∴∠OCA=∠DAC，

∴AD∥CO，

∵CD⊥AD，

∴OC⊥CD，

∵OC是⊙O直径且C在半径外端，

∴CD为⊙O的切线；

（2）解：∵AB=2BO，AB=2BE，

∴BO=BE=CO，

设BO=BE=CO=x，

∴OE=2x，

在Rt△OCE中，

根据勾股定理得：OC2+CE2=OE2，即x2+（ ）2=（2x）2

∴x=1，

∴AE=3，∠E=30°，

∴AD= ．

【解析】（1）如图，连接OC，由AC平分∠DAB得到∠DAC=∠CAB，然后利用等腰三角形的性质得到∠OCA=∠CAB，接着利用平行线的判定得到AD∥CO，而CD⊥AD，由此得到CD⊥AD，最后利用切线的判定定理即可证明CD为⊙O的切线；（2）由AB=2BO，AB=2BE得到BO=BE=CO，设BO=BE=CO=x，所以OE=2x，在Rt△OCE中，利用勾股定理列出关于x的方程，解方程求出x，最后利用三角函数的定义即可求解．
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．