题目内容
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
①2a﹣b=0;
②abc>0;
③4ac﹣b2<0;
④9a+3b+c<0;
⑤关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
⑥8a+c<0.
其中正确的个数是( )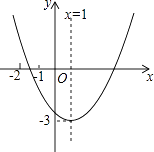
A.2
B.3
C.4
D.5
【答案】C
【解析】解:①抛物线的对称轴为x=﹣ ![]() =1,b=﹣2a,
=1,b=﹣2a,
所以2a+b=0,故①错误;
②抛物线开口向上,得:a>0;抛物线的对称轴为x=﹣ ![]() >0故b<0;抛物线交y轴于负半轴,得:c<0;所以abc>0;故②正确;
>0故b<0;抛物线交y轴于负半轴,得:c<0;所以abc>0;故②正确;
③由图知:抛物线与x轴有两个不同的交点,则△=b2﹣4ac>0,∴4ac﹣b2<0,故③正确;
④根据抛物线的对称轴方程可知:(﹣1,0)关于对称轴的对称点是(3,0);
当x=﹣1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确;
⑤二次函数y=ax2+bx+c的最小值为﹣3,所以关于x的一元二次方程ax2+bx+c+3=0有两个相等的实数根,故⑤正确;
⑥由图知:当x=﹣2时y>0,所以4a﹣2b+c>0,因为b=﹣2a,所以4a+4a+c>0,即8a+c>0,故⑥错误;
所以这结论正确的有②③④⑤4个.
故选C.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目