题目内容
【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB.
∠ACB.
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∴∠BOC=180°-(∠1+∠2)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A
∠A
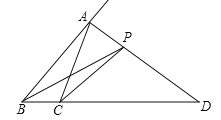
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.

【答案】∠BOC=![]() ∠A.
∠A.
【解析】试题分析:根据提供的信息,由三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠A的关系;
试题解析:解:结论:∠BOC=![]() ∠A.理由如下:
∠A.理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACD.又∵∠ACD是△ABC的一外角,∴∠ACD=∠A+∠ABC,∴∠2=
∠ACD.又∵∠ACD是△ABC的一外角,∴∠ACD=∠A+∠ABC,∴∠2=![]() (∠A+∠ABC)=
(∠A+∠ABC)=![]() ∠A+∠1.∵∠2是△BOC的一外角,∴∠BOC=∠2﹣∠1=
∠A+∠1.∵∠2是△BOC的一外角,∴∠BOC=∠2﹣∠1=![]() ∠A+∠1﹣∠1=
∠A+∠1﹣∠1=![]() ∠A,即∠BOC=
∠A,即∠BOC=![]() ∠A.
∠A.


练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目