Question

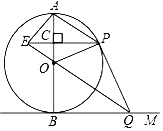
【题目】如图，AB是⊙O的直径，BM切⊙O于点B，点P是⊙O上的一个动点（点P不与A，B两点重合），连接AP，过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ，OP，AE．

（1）求证：直线PQ为⊙O的切线；

（2）若直径AB的长为4．

①当PE＝　 　时，四边形BOPQ为正方形；

②当PE＝　 　时，四边形AEOP为菱形．

Answer 1

【答案】（1）见解析；（2）①2；②2

【解析】

（1）根据切线的性质得∠OBQ＝90°，根据平行线的性质得∠APO＝∠POQ，∠OAP＝∠BOQ，加上∠OPA＝∠OAP，则∠POQ＝∠BOQ，于是根据“SAS”可判断△BOQ≌△POQ，得到∠OPQ＝∠OBQ＝90°，根据切线的判定即可得证；

（2）①由（1）得到∠OPQ＝∠OBQ＝90°，由于OB＝OP，所以当∠BOP＝90°，四边形OPQB为正方形，此时点C、点E与点O重合，于是PE＝PO＝2；②根据菱形的判定，当OC＝AC，PC＝EC，四边形AEOP为菱形，则OC＝OA＝1，然后利用勾股定理计算出PC，从而得到PE的长．

（1）证明：∵OQ∥AP，

∴∠BOQ＝∠OAP，∠POQ＝∠APO，

又∵OP＝OA，

∴∠APO＝∠OAP，

∴∠POQ＝∠BOQ，

在△BOQ与△POQ中，

，

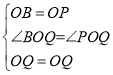∴△BOQ≌△POQ（SAS），

∴∠OPQ＝∠OBQ＝90°，

∵点P在⊙O上，

∴PQ是⊙O的切线；

（2）解：①∵∠OBQ＝∠OPQ＝90°，

∴当∠BOP＝90°，四边形OPQB为矩形，

而OB＝OP，则四边形OPQB为正方形，此时点C、点E与点O重合，PE＝PO＝AB＝2；

②∵PE⊥AB，

∴当OC＝AC，PC＝EC，四边形AEOP为菱形，

∵OC＝OA＝1，

∴，

∴PE＝2PC＝2．

故答案为：2；2．