题目内容
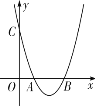
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与y轴交于点
,与y轴交于点![]() .
.
(1)求二次函数的解析式;
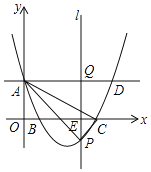
(2)若点P为抛物线上的一点,点F为对称轴上的一点,且以点ABPF为顶点的四边形为平行四边形,求点P的坐标;
(3)点E是二次函数第四象限图象上一点,过点E作x轴的垂线,交直线BC于点D,求四边形![]() 面积的最大值及此时点E的坐标.
面积的最大值及此时点E的坐标.
【答案】(1)![]() ;(2)点P的坐标为
;(2)点P的坐标为![]() 或
或![]() ;(3)四边形
;(3)四边形![]() 面积的最大值为
面积的最大值为![]() ,此时点E的坐标为
,此时点E的坐标为![]() .
.
【解析】
解:(1)将点![]() 代入
代入![]() 中,
中,
得![]() , 解得
, 解得![]() .
.
∴二次函数的解析式为![]() ;
;
(2)如解图①,当以AB为边时,
∵以点ABPF为顶点的四边形为平行四边形,
![]() .
.
已知点![]() ,
,
![]() ,对称轴
,对称轴![]() .
.
设点![]() ,点
,点![]() ,
,
则![]() ,解得
,解得![]() 或
或![]() ,
,
∵点![]() 在二次函数的图象上,
在二次函数的图象上,
∴将![]() 或
或![]() 代入
代入![]() 中.
中.
∴点![]() ;
;
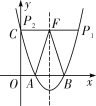
图①
如图②,当以AB为对角线时,设AB与PF的交点为M,
∵以点ABPF为顶点的四边形是平行四边形,
![]() .
.
![]() ,
,
∴点![]() ,∵点F在对称轴上,
,∵点F在对称轴上,
∴F点的横坐标为2.
∴P点的横坐标为2.
将![]() 代入
代入![]() 中,得
中,得![]() ,
,
∴点![]() .
.
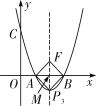
图②
综上所述,以点ABPF为顶点的四边形为平行四边形时,点P的坐标为![]() 或
或![]() ;
;
(3)如解图③,设直线BC的解析式为![]() ,
,
将![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]() 的坐标为
的坐标为![]() .
.
把![]() 和
和![]() 代入
代入![]() 中得
中得![]() 解得
解得![]()
∴直线BC的解析式为![]() .
.
设![]()
则![]()
由![]() 得
得![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() .
.![]() .
.
则四边形![]() 面积的最大值为
面积的最大值为![]() ,此时点E的坐标为
,此时点E的坐标为![]() .
.
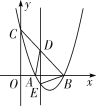
图③

练习册系列答案
相关题目