Question

【题目】如图，已知直线∥，且和，分别交于A，B两点，和，相交于C，D两点，点P在直线AB上，

（1）当点P在A，B两点间运动时，问∠1，∠2，∠3之间的关系是否发生变化？如果不发生变化它们之间满足什么关系？并说明理由；

（2）如果点P在A，B两点外侧运动时，试探究∠ACP，∠BDP，∠CPD之间的关系，并说明理由．

Answer 1

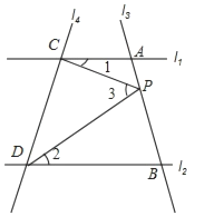
【答案】（1）∠3=∠1+∠2，见解析；（2）∠CPD=∠BDP-∠ACP或∠CPD =∠ACP -∠BDP.

【解析】

（1）过点P作l1的平行线，根据平行线的性质进行解题；
（2）过点P作l1的平行线PF，由平行线的性质可得出l1∥l2∥PF，由此即可得出结论．

解：（1）如图1，过点P作PQ∥l1，

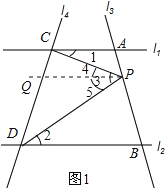
∵PQ∥l1，
∴∠1=∠4（两直线平行，内错角相等），
∵PQ∥l1，l1∥l2（已知），
∴PQ∥l2（平行于同一条直线的两直线平行），
∴∠5=∠2（两直线平行，内错角相等），
∵∠3=∠4+∠5，
∴∠3=∠1+∠2（等量代换）；

（2）如图2，过P点作PF∥BD交CD于F点，

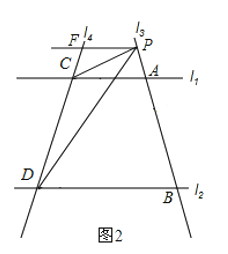
∵AC∥BD，
∴PF∥AC，
∴∠ACP=∠CPF，∠BDP=∠DPF，
∴∠CPD=∠DPF-∠CPF=∠BDP-∠ACP；
如图③，过P点作PF∥BD交CD于F点，

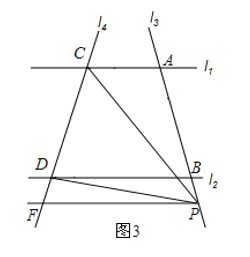
∵AC∥BD，
∴PF∥AC，
∴∠ACP=∠CPF，∠BDP=∠DPF，
∴∠CPD=∠CPF - ∠DPF =∠ACP -∠BDP；