题目内容
【题目】已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
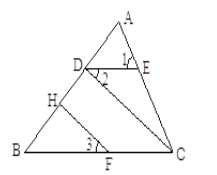
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3=
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴ ( )
∵CD∥FH
∴∠BHF=∠BDC=90°( )
即CD⊥AB( )
【答案】同位角相等,两直线平行;∠BCD,两直线平行,内错角相等;∠BCD;同位角相等,两直线平行;两直线平行,同位角相等;∠BHF=90°,垂直的定义;两直线平行,同位角相等;垂直的定义.
【解析】
先根据,∠1=∠ACB得出DE∥BC,故可得出∠2=∠BCD,根据∠2=∠3得出∠3=∠BCD,所以CD∥FH,再由垂直的定义得出∠BHF=90°由平行线的性质即可得出结论.
∵∠1=∠ACB(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠2=∠BCD.(两直线平行,内错角相等).
∵∠2=∠3(已知),
∴∠3=∠BCD
∴CD∥FH(同位角相等,两直线平行),
∴∠BDC=∠BHF(两直线平行,同位角相等)
又∵FH⊥AB(已知),
∴∠BHF=90°(垂直的定义).
∵CD∥FH
∴∠BDC=∠BHF=90°,(两直线平行,同位角相等)
∴CD⊥AB(垂直的定义).
故答案为:同位角相等,两直线平行;∠BCD,两直线平行,内错角相等;∠BCD;同位角相等,两直线平行;两直线平行,同位角相等;∠BHF=90°;垂直的定义;两直线平行,同位角相等;垂直的定义.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目