Question

【题目】如图，在平面直角坐标系中，△ABC的顶点A在第一象限，点B，C的坐标为（2，1），（6，1），∠BAC=90°，AB=AC，直线AB交x轴于点P．若△ABC与△A'B'C'关于点P成中心对称，则点A'的坐标为 ．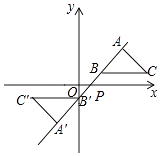

Answer 1

【答案】（﹣2,﹣3）
【解析】如图

，

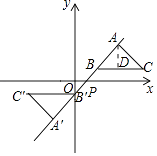点B，C的坐标为（2，1），（6，1），得

BC=4．

由∠BAC=90°，AB=AC，

得AB=2 ，∠ABD=45°，

∴BD=AD=2，

A（4，3），

设AB的解析式为y=kx+b，将A，B点坐标代入，得

，

解得 ，

AB的解析式为y=x﹣1，

当y=1时，x=1，即P（1，0），

由中点坐标公式，得

xA′=2xP﹣xA=2﹣4=﹣2，

yA′=2yA′﹣yA=0﹣3=﹣3，

A′（﹣2，﹣3）．

所以答案是：（﹣2，﹣3）．

【考点精析】解答此题的关键在于理解中心对称及中心对称图形的相关知识，掌握如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形．