题目内容
【题目】已知点P是线段AB上与点A不重合的一点,且AP<PB.AP绕点A逆时针旋转角α(0°<α≤90°)得到AP1 , BP绕点B顺时针也旋转角α得到BP2 , 连接PP1、PP2 . 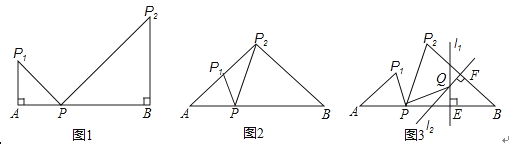
(1)如图1,当α=90°时,求∠P1PP2的度数;
(2)如图2,当点P2在AP1的延长线上时,求证:△P2P1P∽△P2PA;
(3)如图3,过BP的中点E作l1⊥BP,过BP2的中点F作l2⊥BP2 , l1与l2交于点Q,连接PQ,求证:P1P⊥PQ.
【答案】
(1)
解:由旋转的性质得:AP=AP1,BP=BP2.
∵α=90°,
∴△PAP1和△PBP2均为等腰直角三角形,
∴∠APP1=∠BPP2=45°,
∴∠P1PP2=180°﹣∠APP1﹣∠BPP2=90°.
(2)
解:
证明:由旋转的性质可知△PAP1和△PBP2均为顶角为α的等腰三角形,
∴∠APP1=∠BPP2=90°﹣![]() ,
,
∴∠P1PP2=180°﹣(∠APP1+∠BPP2)=180°﹣2(90°﹣![]() )=α,
)=α,
在△PP2P1和△P2PA中,∠P1PP2=∠PAP2=α,
又∵∠PP2P1=∠AP2P,
∴△P2P1P∽△P2PA.
(3)
解:证明:如图,连接QB.
∵l1,l2分别为PB,P2B的中垂线,
∴EB=![]() BP,FB=
BP,FB=![]() BP2.
BP2.
又BP=BP2,
∴EB=FB.
在Rt△QBE和Rt△QBF中,
![]() ,
,
∴Rt△QBE≌Rt△QBF,
∴∠QBE=∠QBF=![]() ∠PBP2=
∠PBP2=![]() ,
,
由中垂线性质得:QP=QB,
∴∠QPB=∠QBE=![]() ,
,
由(2)知∠APP1=90°﹣![]() ,
,
∴∠P1PQ=180°﹣∠APP1﹣∠QPB=180°﹣(90°﹣![]() )﹣
)﹣![]() =90°,
=90°,
即 P1P⊥PQ.

【解析】(1)利用旋转的性质以及等腰直角三角形得出∠APP1=∠BPP2=45°,进而得出答案;
(2)根据题意得出△PAP1和△PBP2均为顶角为α的等腰三角形,进而得出∠P1PP2=∠PAP2=α,求出△P2P1P∽△P2PA;
(3)首先连结QB,得出Rt△QBE≌Rt△QBF,利用∠P1PQ=180°﹣∠APP1﹣∠QPB求出即可.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 阅读快车系列答案
阅读快车系列答案