Question

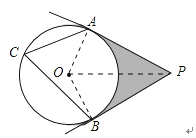
【题目】如图，PA，PB分别与⊙O相切于A，B两点，∠ACB=60°．

（1）求∠P的度数
（2）若⊙O的半径长为4cm，求图中阴影部分的面积

Answer 1

【答案】
（1）

解：连接OA、OB，

∵PA、PB是⊙O的切线，

∴OA⊥AP，OB⊥BP，

∴∠OAP=∠OBP=90°，

又∵∠AOB=2∠C=120°，

∴∠P=360°﹣（90°+90°+120°）=60°．

∴∠P=60°．

（2）

解：连接OP，如图所示：

∵PA、PB是⊙O的切线，

∴∠APO=∠APB=30°，

在RT△APO中，tan30°=，

∴AP===4cm，

∴S阴影=2S△AOP﹣S扇形=2×（×4×﹣）=（16﹣）（cm2）．

【解析】（1）由PA与PB都为圆O的切线，利用切线的性质得到OA垂直于AP，OB垂直于BP，可得出两个角为直角，再由同弧所对的圆心角等于所对圆周角的2倍，由已知∠C的度数求出∠AOB的度数，在四边形PABO中，根据四边形的内角和定理即可求出∠P的度数．
（2）由S阴影=2×（S△PAO﹣S扇形）则可求得结果．
此题考查了圆的综合应用，涉及知识点有切线性质，圆心角和圆周角，四边形内角和以及扇形面积的 求法。