Question

【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，已知，CD=8，AE=2，求⊙O的半径．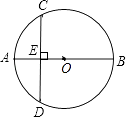

Answer 1

【答案】解：连接OC， ∵AB是⊙O的直径，CD⊥AB，
∴CE= CD=4，∠OEC=90°，
设OC=OA=x，则OE=x﹣2，
根据勾股定理得：CE2+OE2=OC2 ，
即42+（x﹣2）2=x2 ，
解得x=5，
所以⊙O的半径为5．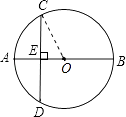

【解析】连接OC，根据垂径定理求出CE的长和∠OEC的度数，设OC=OA=x，根据勾股定理列出方程，解方程即可．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对垂径定理的理解，了解垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．