题目内容
【题目】如图，在四边形ABCD中，AB∥CD，且AB=2CD，E，F分别是AB，BC的中点，EF与BD交于点H．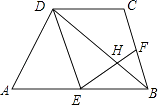 
（1）求证：△EDH∽△FBH；
（2）若BD=6，求DH的长．
【答案】
（1）证明：∵在四边形ABCD中，AB∥CD，且AB=2CD，E，是AB的中点，
∴DC= 
AB=EB，DC∥BE，
∴四边形DCBE是平行四边形，
∴FB∥DE，
∴△EDH∽△FBH
（2）解：由（1）知，BC∥DE，BC=DE，
∵FB= BC，
∴FB= DE．
∵△EDH∽△FBH，
∴ 
=2．
∵DH+HB=6，
∴DH=4
【解析】（1）先根据题意得出四边形DCBE是平行四边形，再由平行四边形的性质得出FB∥DE，故可得出∠FBH=∠EDH，∠DEH=∠BFH，进而可得出结论；（2）先有平行四边形的性质得出BC∥DE，BC=DE，再由△EDH∽△FBH可得出结论．
【考点精析】掌握三角形中位线定理和相似三角形的判定与性质是解答本题的根本，需要知道连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
