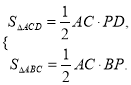题目内容
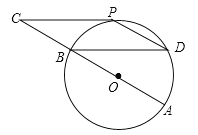
【题目】我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO2﹣BO2的值，可记为AB△AC=AO2﹣BO2 ．
（1）在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC= ， OC△OA=；
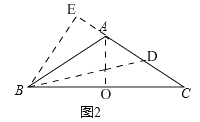
（2）如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；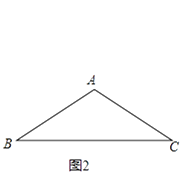
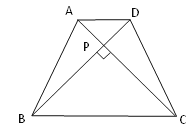
（3）如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON= 
AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．
【答案】
（1）0；7
（2）
解：①如图2，取BC的中点O，连接AO，
∵AB=AC，
∴AO⊥BC，
在△ABC中，AB=AC，∠BAC=120°，
∴∠ABC=30°，
在Rt△AOB中，AB=4，∠ABC=30°，
∴AO=2，OB=2 
，
∴AB△AC=AO2﹣BO2=4﹣12=﹣8，
②取AC的中点D，连接BD，
∴AD=CD= 
AC=2，
过点B作BE⊥AC交CA的延长线于E，
在Rt△ABE中，∠BAE=180°﹣∠BAC=60°，
∴∠ABE=30°，
∵AB=4，
∴AE=2，BE=2 ，
∴DE=AD+AE=4，
在Rt△BED中，根据勾股定理得，BD= 
= 
=2 
，
∴BA△BC=BD2﹣CD2=24；
（3）
解：如图3，
设ON=x，OB=OC=y，
∴BC=2y，OA=3x，
∵AB△AC=14，
∴OA2﹣OB2=14，
∴9x2﹣y2=14①，
取AN的中点D，连接BD，
∴AD=DB= AN= × 
OA=ON=x，
∴OD=ON+DN=2x，
在Rt△BOD中，BD2=OB2+OD2=y2+4x2，
∵BN△BA=10，
∴BD2﹣DN2=10，
∴y2+4x2﹣x2=10，
∴3x2+y2=10②
联立①②得， 
或 
（舍），
∴BC=4，OA=3 
，
∴S△ABC= BC×AO=6 ．
【解析】解：①∵∠BAC=90°，AB=8，AC=6，
∴BC=10，
∵点O是BC的中点，
∴OA=OB=OC= BC=5，
∴AB△AC=AO2﹣BO2=25﹣25=0，②如图1，
取AC的中点D，连接OD，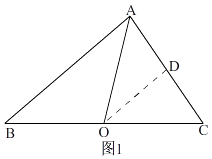
∴CD= AC=3，
∵OA=OC=5，
∴OD⊥AC，
在Rt△COD中，OD= 
=4，
∴OC△OA=OD2﹣CD2=16﹣9=7，
故答案为0，7；
（1）①先根据勾股定理求出BC=10，再利用直角三角形的性质得出OA=OB=OC=5，最后利用新定义即可得出结论；②再用等腰三角形的性质求出CD=3，再利用勾股定理求出OD，最后用新定义即可得出结论；（2）①先利用含30°的直角三角形的性质求出AO=2，OB=2 ，再用新定义即可得出结论；②先构造直角三角形求出BE，AE，再用勾股定理求出BD，最后用新定义即可得出结论；（3）先构造直角三角形，表述出OA，BD2 ， 最后用新定义建立方程组求解即可得出结论．
