题目内容
如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C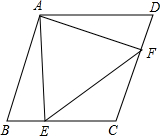 运动.给出以下四个结论:
运动.给出以下四个结论:①AE=AF;
②∠CEF=∠CFE;
③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;
④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.
上述结论中正确的序号有
分析:根据菱形的性质对各个结论进行验证从而得到正确的序号.
解答: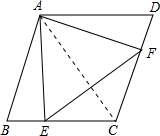 解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,
解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,
∴BE=DF,
∵AB=AD,∠B=∠D,
∴△ABE≌△ADF,
∴AE=AF,①正确;
∴CE=CF,
∴∠CEF=∠CFE,②正确;
∵在菱形ABCD中,∠B=60°,
∴AB=BC,
∴△ABC是等边三角形,
∴当点E,F分别为边BC,DC的中点时,BE=
AB,DF=
AD,
∴△ABE和△ADF是直角三角形,且∠BAE=∠DAF=30°,
∴∠EAF=120°-30°-30°=60°,
∴△AEF是等边三角形,③正确;
∵△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积=
AB2-
BE•AB×
×2-
×
×(AB-BE)2=-
BE2+
AB2,
∴△AEF的面积是BE的二次函数,
∴当BE=0时,△AEF的面积最大,④错误.
故正确的序号有①②③.
 解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,
解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,∴BE=DF,
∵AB=AD,∠B=∠D,
∴△ABE≌△ADF,
∴AE=AF,①正确;
∴CE=CF,
∴∠CEF=∠CFE,②正确;
∵在菱形ABCD中,∠B=60°,
∴AB=BC,
∴△ABC是等边三角形,
∴当点E,F分别为边BC,DC的中点时,BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABE和△ADF是直角三角形,且∠BAE=∠DAF=30°,
∴∠EAF=120°-30°-30°=60°,
∴△AEF是等边三角形,③正确;
∵△AEF的面积=菱形ABCD的面积-△ABE的面积-△ADF的面积-△CEF的面积=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
∴△AEF的面积是BE的二次函数,
∴当BE=0时,△AEF的面积最大,④错误.
故正确的序号有①②③.
点评:本题考查了菱形的性质、全等三角形的判定和等边三角形的判定.

练习册系列答案
相关题目
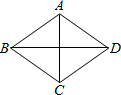 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
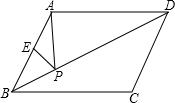
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.