题目内容

如图，在菱形ABCD中，AE⊥BC，垂足为F，EC=1，∠B=30°，求菱形ABCD的周长．
分析：首先表示出BC与AB的关系，进而得出AB的长，即可得出答案．
解答：解：在Rt△ABE中，BE=ABcosB=
3
2
AB，
∴BC=BE+CE=
3
2
AB+1=AB，
∴AB=
1
1-
3
2
=4+2
3
，
∴菱形的周长为：4AB=16+8
3
．
点评：此题主要考查了菱形的性质以及锐角三角函数关系等知识，根据已知得出AB的长是解题关键．
练习册系列答案
相关题目
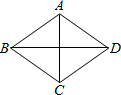精英家教网如图：在菱形ABCD中，AC=6，BD=8，则菱形的边长为（　　）
A、5B、10C、6D、8
如图，在菱形ABCD中，∠ABC=60°，E为AB边的中点，P为对角线BD上任意一点，AB=4，则PE+PA的最小值为
 
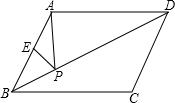
．精英家教网
（2012•河南）如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．
（1）求证：四边形AMDN是平行四边形；
（2）填空：①当AM的值为
1
1
时，四边形AMDN是矩形；
           ②当AM的值为
2
2
时，四边形AMDN是菱形．
（2013•攀枝花）如图，在菱形ABCD中，DE⊥AB于点E，cosA=
35
，BE=4，则tan∠DBE的值是
2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网