题目内容
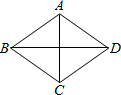如图：在菱形ABCD中，AC=6，BD=8，则菱形的边长为（ ）| A、5 | B、10 | C、6 | D、8 |
分析：根据菱形的性质：菱形的对角线互相垂直平分，且每一条对角线平分一组对角，可知每个直角三角形的直角边，根据勾股定理可将菱形的边长求出．
解答：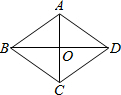
解：设AC与BD相交于点O，
由菱形的性质知：AC⊥BD，OA=
AC=3，OB=
BD=4
在Rt△OAB中，AB=
=
=5
所以菱形的边长为5．
故选A．
解：设AC与BD相交于点O，由菱形的性质知：AC⊥BD，OA=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OAB中，AB=
| OA2+OB2 |
| 32+42 |
所以菱形的边长为5．
故选A．
点评：本题主要利用菱形的对角线互相垂直平分及勾股定理来解决．
练习册系列答案
相关题目
ME交射线CD于点N，连接MD、AN．
（2013•攀枝花）如图，在菱形ABCD中，DE⊥AB于点E，cosA=
如图，在菱形ABCD中，AE⊥BC，垂足为F，EC=1，∠B=30°，求菱形ABCD的周长．