题目内容
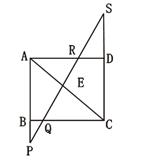
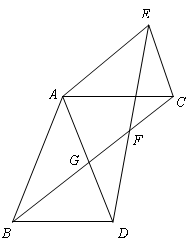
如图1,在△ABC中,AB=AC, . 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
. 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
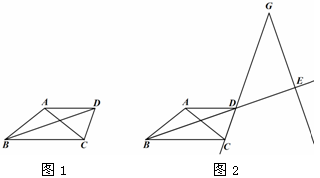
(1)求证: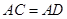 ;
;
(2)点 为线段
为线段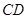 延长线上一点,将射线GC绕着点G逆时针旋转
延长线上一点,将射线GC绕着点G逆时针旋转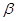 ,与射线BD交于点E.
,与射线BD交于点E.
①若 ,
, ,如图2所示,求证:
,如图2所示,求证: ;
;
②若 ,
, ,请直接写出
,请直接写出 的值(用含
的值(用含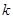 的代数式表示).
的代数式表示).
 . 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
. 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD. 
(1)求证:
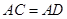 ;
;(2)点
 为线段
为线段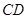 延长线上一点,将射线GC绕着点G逆时针旋转
延长线上一点,将射线GC绕着点G逆时针旋转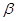 ,与射线BD交于点E.
,与射线BD交于点E.①若
 ,
, ,如图2所示,求证:
,如图2所示,求证: ;
;②若
 ,
, ,请直接写出
,请直接写出 的值(用含
的值(用含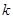 的代数式表示).
的代数式表示).(1)先根据角平分线的性质结合平行线的性质证得 ,再结合
,再结合 即可证得结论;(2)①过
即可证得结论;(2)①过 作
作 于点
于点 ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得 ,根据三角形的内角和定理可得
,根据三角形的内角和定理可得 ,由(1)得
,由(1)得 ,即可得到点
,即可得到点 、
、 、
、 在以
在以 为圆心,
为圆心, 为半径的圆上,根据圆周角定理可得
为半径的圆上,根据圆周角定理可得 ,即得
,即得 ,然后证得△
,然后证得△ ∽△
∽△ ,再根据相似三角形的性质即可证得结论;②
,再根据相似三角形的性质即可证得结论;② .
.
 ,再结合
,再结合 即可证得结论;(2)①过
即可证得结论;(2)①过 作
作 于点
于点 ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得 ,根据三角形的内角和定理可得
,根据三角形的内角和定理可得 ,由(1)得
,由(1)得 ,即可得到点
,即可得到点 、
、 、
、 在以
在以 为圆心,
为圆心, 为半径的圆上,根据圆周角定理可得
为半径的圆上,根据圆周角定理可得 ,即得
,即得 ,然后证得△
,然后证得△ ∽△
∽△ ,再根据相似三角形的性质即可证得结论;②
,再根据相似三角形的性质即可证得结论;② .
.试题分析:(1)先根据角平分线的性质结合平行线的性质证得
 ,再结合
,再结合 即可证得结论;(2)①过
即可证得结论;(2)①过 作
作 于点
于点 ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得 ,根据三角形的内角和定理可得
,根据三角形的内角和定理可得 ,由(1)得
,由(1)得 ,即可得到点
,即可得到点 、
、 、
、 在以
在以 为圆心,
为圆心, 为半径的圆上,根据圆周角定理可得
为半径的圆上,根据圆周角定理可得 ,即得
,即得 ,然后证得△
,然后证得△ ∽△
∽△ ,再根据相似三角形的性质即可证得结论;②根据①的结论推导可得结果.
,再根据相似三角形的性质即可证得结论;②根据①的结论推导可得结果.(1)∵
 平分
平分 ,
,
∴
 .
.∵
 ∥
∥ ,
,∴
 .
.∴
 .
.∴
 .
.∵
 ,
,∴
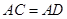 ;
;(2)①过
 作
作 于点
于点 .
.
∴
 .
.∵
 ,
, ,
,∴
 .
.∴
 .
.由(1)得
 .
.∴点
 、
、 、
、 在以
在以 为圆心,
为圆心, 为半径的圆上.
为半径的圆上.∴
 .
.∴
 .
. ∵
 =
=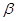 =
=
 ,
,∴
 .
.∴
 .
.∴△
 ∽△
∽△ .
.∵
 ,
, ,
,∴
 =4.
=4.∵
 ∥
∥ ,
,∴
 .
.∴
 ;
;②
 .
.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目

 (m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.
(m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.