题目内容
如图,在□ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
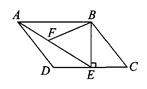
⑴试说明:△ABF∽△EAD;
⑵若AB=8,BE=6,AD=7,求BF的长.

⑴试说明:△ABF∽△EAD;
⑵若AB=8,BE=6,AD=7,求BF的长.
①可通过证明∠BAF=∠AED∠AFB=∠D,∴△ABF∽△EAD ②5.6
试题分析:(1)证明:在平行四边形ABCD中,
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
(2)解:∵BE⊥CD,AB∥CD,∴BE⊥AB.
∴∠ABE=90°.∴AE=
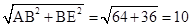
∵△ABF∽△EAD,∴
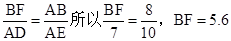
点评:本题主要考查了相似三角形的判定和性质,同时也用到了平行四边形的性质和等角的补角相等等知识点.为中考常考题型,要求学生牢固掌握解题技巧。

练习册系列答案
相关题目
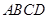 中,
中,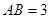 ,
, ,点
,点 在边
在边 上的,过点
上的,过点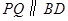 ,交
,交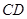 边于
边于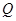 点,再把
点,再把 沿
沿 对折,点
对折,点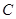 的对应点
的对应点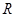 恰好落在
恰好落在 边上,则CP= .
边上,则CP= .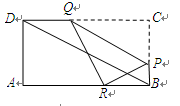
 . 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
. 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD. 
 ;
; 为线段
为线段 延长线上一点,将射线GC绕着点G逆时针旋转
延长线上一点,将射线GC绕着点G逆时针旋转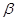 ,与射线BD交于点E.
,与射线BD交于点E. ,
, ,如图2所示,求证:
,如图2所示,求证: ;
; ,
,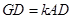 ,请直接写出
,请直接写出 的值(用含
的值(用含 的代数式表示).
的代数式表示).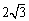 ,∠ACB=90°,∠A=30°,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、E2013,分别记△BCE1、△BCE2、△BCE3、···、△BCE2013的面积为S1、S2、S3、…、S2013.则S2013的大小为( ).
,∠ACB=90°,∠A=30°,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、E2013,分别记△BCE1、△BCE2、△BCE3、···、△BCE2013的面积为S1、S2、S3、…、S2013.则S2013的大小为( ).



