Question

【题目】已知∠AOB=45°，求作∠AOP=22.5°，作法：

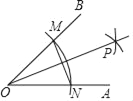
（1）以O为圆心，任意长为半径画弧分别交OA，OB于点N，M；

（2）分别以N，M为圆心，以OM长为半径在角的内部画弧交于点P；

（3）作射线OP，则OP为∠AOB的平分线，可得∠AOP=22.5°

根据以上作法，某同学有以下3种证明思路：

①可证明△OPN≌△OPM，得∠POA=∠POB，可得；

②可证明四边形OMPN为菱形，OP，MN互相垂直平分，得∠POA=∠POB，可得；

③可证明△PMN为等边三角形，OP，MN互相垂直平分，从而得∠POA=∠POB，可得．

你认为该同学以上3种证明思路中，正确的有（　　）

A. ①② B. ①③ C. ②③ D. ①②③

Answer 1

【答案】A

【解析】

①根据SSS可证明△OMP≌△ONP（SSS），得∠POA=∠POB；

②根据四边相等可证明四边形MONP是菱形，可得结论；

③根据线段中垂线的判定和等腰三角形三线合一可得结论．

①由作图得：OM=ON，PM=PN．

∵OP=OP，∴△OMP≌△ONP（SSS），∴∠POA=∠POB；

故①正确；

②由作图得：OM=ON=PM=PN，∴四边形MONP是菱形，∴OP平分∠MON，∴∠POA=∠POB，故②正确；

③∵PM=PN，但MN不一定与PM相等，∴△PMN不一定是等边三角形，正确证明：∵OM=ON，PM=PN，∴OP是MN的中垂线，∴OP⊥MN，∴∠POA=∠POB，故③不正确．

故选A．