题目内容
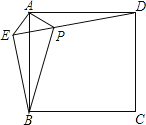
【题目】如图,点E是正方形ABCD外一点,连接AE、BE和DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=3.下列结论:①△APD≌△AEB;②EB⊥ED;③点B到直线AE的距离为![]() ;④S正方形ABCD=8+
;④S正方形ABCD=8+![]() .则正确结论的个数是( )
.则正确结论的个数是( )
A.1B.2C.3D.4
【答案】C
【解析】
①易知AE=AP,AB=AD,所以只需证明∠EAB=∠PAD即可用SAS说明△APD≌△AEB;
②易知∠AEB=∠APD=135°,则∠BEP=∠AEB﹣∠AEP=135°﹣45°=90°,所以EB⊥ED;
③在Rt△BEP中利用勾股定理求出BE值为![]() ,根据垂线段最短可知B到直线AE的距离小于
,根据垂线段最短可知B到直线AE的距离小于![]() ;则③错误;
;则③错误;
④要求正方形的面积,则需知道正方形一条边的平方值即可,所以在△AEB中,∠AEB=135°,AE=1,BE=![]() ,过点A作AH⊥BE交BE延长线于H点,在Rt△AHB中利用勾股定理AB2=BH2+AH2即可.
,过点A作AH⊥BE交BE延长线于H点,在Rt△AHB中利用勾股定理AB2=BH2+AH2即可.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°.
∴∠DAP+∠BAP=90°.
又∠EAP+∠BAP=90°,
∴∠EAP=∠DAP.
又AE=AP,
∴△APD≌△AEB(SAS).
所以①正确;
∵AE=AP,∠EAP=90°,
∴∠APE=∠AEP=45°,
∴∠APD=180°﹣45°=135°.
∵△APD≌△AEB,
∴∠AEB=∠APD=135°,
∴∠BEP=135°﹣45°=90°,
即EB⊥ED,②正确;
在等腰Rt△AEP中,利用勾股定理可得EP=![]() ,
,
在Rt△BEP中,利用勾股定理可得BE=![]() .
.
∵B点到直线AE的距离小于BE,所以点B到直线AE的距离为![]() 是错误的,
是错误的,
所以③错误;
在△AEB中,∠AEB=135°,AE=1,BE=![]() ,
,
如图所示,过点A作AH⊥BE交BE延长线于H点.
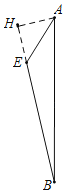
在等腰Rt△AHE中,可得AH=HE=![]() AE=
AE=![]() .
.
所以BH=![]() .
.
在Rt△AHB中利用勾股定理可得AB2=BH2+AH2,
即AB2=(![]() )2+(
)2+(![]() )2=8+
)2=8+![]() ,
,
所以S正方形ABCD=8+![]() .
.
所以④正确.
所以只有①和②、④的结论正确.
故选:C.