Question

【题目】（1）如图1，AB∥CD，点E是在AB、CD之间，且在BD的左侧平面区域内一点，连结BE、DE．求证：∠E=∠ABE+∠CDE．

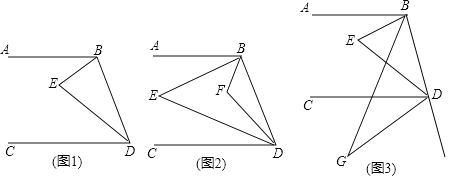
（2）如图2，在（1）的条件下，作出∠EBD和∠EDB的平分线，两线交于点F，猜想∠F、∠ABE、∠CDE之间的关系，并证明你的猜想．

（3）如图3，在（1）的条件下，作出∠EBD的平分线和△EDB的外角平分线，两线交于点G，猜想∠G、∠ABE、∠CDE之间的关系，并证明你的猜想．

Answer 1

【答案】（1）见解析（2）见解析（3）2∠G=∠ABE+∠CDE

【解析】

（1）利用平行线的性质即可得出结论；

（2）先判断出∠EBD+∠EDB=180°-（∠ABE+∠CDE），进而得出∠DBF+∠BDF=90°- （∠ABE+∠CDE），最后用三角形的内角和即可得出结论；

（3）先由（1）知，∠BED=∠ABE+∠CDE，再利用角平分线的意义和三角形外角的性质即可得出结论．

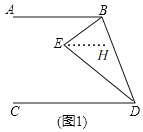
（1）如图，

过点E作EH∥AB，

∴∠BEH=∠ABE，

∵EH∥AB，CD∥AB，

∴EH∥CD，

∴∠DEH=∠CDE，

∴∠BED=∠BEH+∠DEH=∠ABE+∠CDE；

（2）2∠F-（∠ABE+∠CDE）=180°，

理由：由（1）知，∠BED=∠ABE+∠CDE，

∵∠EDB+∠EBD+∠BED=180°，

∴∠EBD+∠EDB=180°-∠BED=180°-（∠ABE+∠CDE），

∵BF，DF分别是∠DBE，∠BDE的平分线，

∴∠EBD=2∠DBF，∠EDB=2∠BDF，

∴2∠DBF+2∠BDF=180°-（∠ABE+∠CDE），

∴∠DBF+∠BDF=90°-（∠ABE+∠CDE），

在△BDF中，∠F=180°-（∠DBF+∠BDF）=180°-[90°-（∠ABE+∠CDE）]=90°+（∠ABE+∠CDE），

即：2∠F-（∠ABE+∠CDE）=180°；

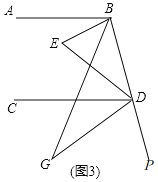
（3）2∠G=∠ABE+∠CDE，理由：如图3，

由（1）知，∠BED=∠ABE+∠CDE，

∵BG是∠EBD的平分线，

∴∠DBE=2∠DBG，

∵DG是∠EDP的平分线，

∴∠EDP=2∠GDP，

∴∠BED=∠EDP-∠DBE=2∠GDP-2∠DBG=2（∠GDP-∠DBG），

∴∠GDP-∠DBG=∠BED=（∠ABE+∠CDE）

∴∠G=∠GDP-∠DBG=（∠ABE+∠CDE），

∴2∠G=∠ABE+∠CDE．