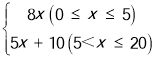题目内容
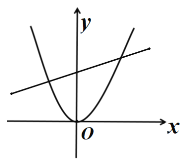
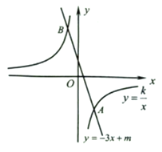
【题目】如图,直线![]() 向上平移2个单位,得到直线
向上平移2个单位,得到直线![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 的一个交点
的一个交点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)直线![]() 与双曲线
与双曲线![]() 的另一个交点为
的另一个交点为![]() ,求坐标原点
,求坐标原点![]() 到线段
到线段![]() 的距离.
的距离.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据平移的原则得出m的值,并计算点A的坐标,因为A在反比例函数的图象上,代入可以求k的值;
(2)画出两函数图象,根据交点坐标写出解集;
(3)求得直线与坐标轴的交点坐标,利用面积法即可求解.
(1)∵![]() 向上平移2个单位得到:
向上平移2个单位得到:
![]() ,
,
∴![]() ,
,
∵![]() 过点
过点![]() ,且点
,且点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴A的坐标为(1,-2),
把![]() 代入
代入![]() ,得:
,得:![]() ;
;
(2)由直线![]() 与双曲线
与双曲线![]() 相交,
相交,
得:![]() ,
,
解之得:![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以交点A的坐标为(1,-2),B的坐标为(![]() ,3),
,3),
结合图像可得:当![]() 或
或![]() 时直线
时直线![]() 在双曲线
在双曲线![]() 的下方,
的下方,
∴当![]() 时,求
时,求![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ;
;
(3)直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点C、D,
轴交于点C、D,
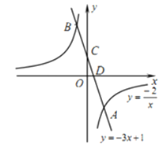
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
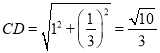 ,
,
∴点![]() 到线段
到线段![]() 的距离:
的距离:![]() .
.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目