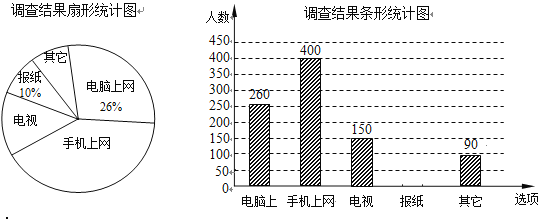
题目内容
【题目】若![]() 和
和![]() 均为等腰三角形,且
均为等腰三角形,且![]() .
.
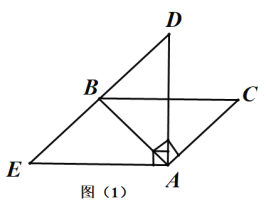
(1)如图(1),点B是![]() 的中点,判定四边形
的中点,判定四边形![]() 的形状,并说明理由;
的形状,并说明理由;
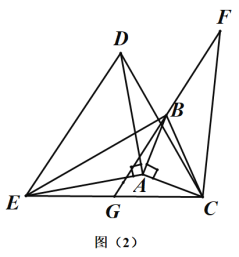
(2)如图(2),若点G是![]() 的中点,连接
的中点,连接![]() 并延长至点F,使
并延长至点F,使![]() .求证:①
.求证:①![]() ,②
,②![]() .
.
【答案】(1)四边形BEAC是平行四边形,证明见解析;(2)①见解析;②见解析
【解析】
(1)利用等腰直角三角形的性质证得![]() ,
,![]() ,推出
,推出![]() ,再根据平行于同一直线的两直线平行即可推出结论;
,再根据平行于同一直线的两直线平行即可推出结论;
(2)①利用“SAS”证得![]() ,即可证明结论;
,即可证明结论;
②延长![]() 至点H,使
至点H,使![]() ,证得
,证得![]() ,推出
,推出![]() ,利用①的结论即可证明
,利用①的结论即可证明![]() .
.
(1)证明:四边形![]() 是平行四边形.
是平行四边形.
理由如下:
∵![]() 为等腰三角形且
为等腰三角形且![]() ,
,
∴![]() ,
,
∵B是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() 是等腰三角形,
是等腰三角形,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
(2)证明:①∵![]() 和
和![]() 为等腰三角形,
为等腰三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ;
;
②延长![]() 至点H,使
至点H,使![]() .
.
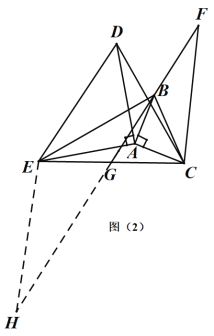
∵G是![]() 中点,
中点,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的![]() 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 |
| 3 |
| |
频率 | 0.05 | 0.10 |
| 0.15 | 1 |
表中![]() 组的频率
组的频率![]() 满足
满足![]() .
.
下面有四个推断:
①表中![]() 的值为20;
的值为20;
②表中![]() 的值可以为7;
的值可以为7;
③这![]() 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在![]() 组;
组;
④这![]() 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④