题目内容
【题目】某企业接到一批产品的生产任务,按要求必须在20天内完成,已知每件产品的售价为65元,工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=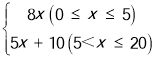 .
.
(1)工人甲第几天生产的产品数量为100件?
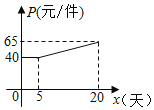
(2)设第x天(0≤x≤20)生产的产品成本为P元/件,P与x的函数图象如图,工人甲第x天创造的利润为W元.
①求P与x的函数关系式;
②求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
【答案】(1)18;(2)①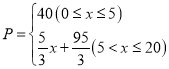 ;②第9天时,利润最大,最大利润是1008
;②第9天时,利润最大,最大利润是1008![]() 元
元
【解析】
(1)将100代入原关系式分别求出各自情况下的x的值,由此进一步根据题意分析判断即可;
(2)①根据函数图像分![]() 以及
以及![]() 两种情况,并且当
两种情况,并且当![]() 时利用待定系数法求出解析式即可;②同样,根据题意分
时利用待定系数法求出解析式即可;②同样,根据题意分![]() 以及
以及![]() 两种情况得出各自情况下的函数关系式,最后根据关系式进一步分析即可.
两种情况得出各自情况下的函数关系式,最后根据关系式进一步分析即可.
(1)当![]() 时,
时,![]() ,则令8x=100,得x=12.5(舍去),
,则令8x=100,得x=12.5(舍去),
当![]() 时,
时,![]() ,则令5x+10=100,得x=18,
,则令5x+10=100,得x=18,
答:工人甲第18天生产的产品数量为100件;
(2)①由图象可得,
当![]() 时,P=40,
时,P=40,
当![]() 时,设P与x的函数关系式为P=kx+b,
时,设P与x的函数关系式为P=kx+b,
由图象可得:![]() ,
,
解得: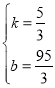 ,
,
即当![]() 时,P与x的函数关系式为P=
时,P与x的函数关系式为P=![]() x+
x+![]() ,
,
由上可得,P与x的函数关系式为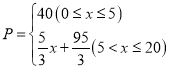 ;
;
②当![]() 时,
时,![]() ,
,
故当x=5时,W取得最大值,此时W=1000;
当![]() 时,
时,![]() ,
,
∴当x=9时,W取得最大值,此时W=1008![]() ,
,
由上可得,W与x的函数关系式是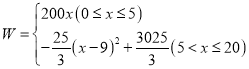 ,
,
答:第9天时,利润最大,最大利润是1008![]() 元.
元.

练习册系列答案
相关题目