Question

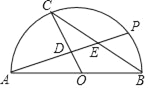
【题目】P是以AB为直径的半圆上一动点（P与A、B不重合），O为圆心，CO⊥AP，OC、BC与AP分别相交于D、E两点，AB＝12．

（1）若∠ABC＝35°，求∠PAB的度数；

（2）若AP平分线段BC，求弦AP的长度；

（3）是否存在点P，使△PBC的面积为整数，如果存在，这样的P点有几个？（直接写出结果，不需写出解题过程．）

Answer 1

【答案】（1）20°（2）8（3）35

【解析】

（1）连接BP，CP，OP，根据圆周角定理和垂径定理进行计算即可；

（2）通过证明三角形全等得出线段CD与OD的关系，进而求出BP，运用勾股定理求解即可；

（3）把S△BPC转化为S△BOP，进而进行分析即可．

如图连接BP，CP，OP，

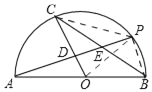
（1）∵∠ABC＝35°，

∴∠AOC＝2∠ABC＝70°，

∵CO⊥AP，

∴∠PAB＝90°﹣70°＝20°；

（2）∵AB是圆的直径，

∴BP⊥AP，

∵CO⊥AP，

∴OC∥BP，∠CDE＝∠BPE＝90°，

∵CE＝BE，∠CED＝∠BEP，

∴△BPE≌△CDE，

∴CD＝BP，

∵AO＝BO，OC∥BP，

∴2OD＝BP，

∴CD＝2OD，

∵OC＝AB＝6，

∴OD＝2，BP＝4，

由勾股定理可得，AP＝＝＝8；

（3）∵OC∥BP，

∴S△BPC＝S△BOP，

∵OB＝6，

∴当点P到OB距离为，，…，6时，S△BPC为整数，

∴这样的P点有35个．

故答案为：（1）20°（2）8（3）35