题目内容
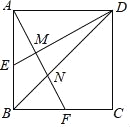
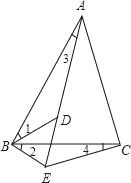
【题目】如图,D为△ABC内一点,E为△ABC外一点,且∠ABC=∠DBE,∠3=∠4.
求证:(1)△ABD∽△CBE;
(2)△ABC∽△DBE.
【答案】(1)证明见解析;(2)证明见解析;
【解析】
(1)根据有两组角对应相等的两个三角形相似可判断△ABD∽△CBE;
(2)先利用得到∠1=∠2得到∠ABC=∠DBE,再利用△ABD∽△CBE得![]() , 根据比例的性质得到
, 根据比例的性质得到![]() , 然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ABC与△DBE相似.
, 然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ABC与△DBE相似.
(1)相似.理由如下:
∵∠1=∠2,∠3=∠4.
∴△ABD∽△CBE;
(2)相似.理由如下:
∵∠1=∠2,
∴∠1+∠DBC=∠2+DBC,即∠ABC=∠DBE,
∵△ABD∽△CBE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴△ABC∽△DBE.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目