题目内容
【题目】如图,正方形ABCD中,以BC为边向正方形内部作等边△BCE,连接AE并延长交CD于F,连接DE,下列结论:①AE=DE;②∠CEF=45°;③AE=EF;④△DEF∽△ABE,其中正确的结论共有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
利用正方形的性质、等边三角形的性质,求出相关角的度数,即可一一解决问题.
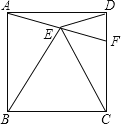
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠ADC=90°,
∵△EBC是等边三角形,
∴BC=BE=CE,∠EBC=∠EBC=∠ECB=60°,
∴∠ABE=∠ECF=30°,
∵BA=BE,EC=CD,
∴∠BAE=∠BEA=∠CED=∠CDE=![]() (180°-30°)=75°,
(180°-30°)=75°,
∴∠EAD=∠EDA=15°,
∴EA=ED,故①正确,
∴∠DEF=∠EAD+∠ADE=30°,
∴∠CEF=∠CED-∠DEF=45°,故②正确,
∵∠EDF=∠AFD=75°,
∴ED=EF,
∴AE=EF,故③正确,
∵∠BAE=∠BEA=∠EDF=∠EFD=75°,
∴△DEF∽△ABE,故④正确,
故选:D.

练习册系列答案
相关题目