题目内容
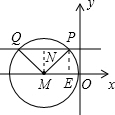
如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是______.(多填或错填的得0分,少填的酌情给分)


作PE⊥X轴于E,MN⊥PQ于N,
∵P(-1,2),
∴OE=1,PE=NM=2,
∵MN⊥PQ,M为圆心,
∴2PN=2QN=PQ,
在△PME中,由勾股定理得:PM2=22+(PM-1)2,
∴PM=
,
由勾股定理得:PN=
=
,
∴PQ=3,∴②正确;
Q(-4,2),∴①正确;
△MPQ的面积是
×3×2=3,∴③正确;
OM=1+
=
,∴④错误;
故答案为:①②③.
∵P(-1,2),
∴OE=1,PE=NM=2,
∵MN⊥PQ,M为圆心,
∴2PN=2QN=PQ,
在△PME中,由勾股定理得:PM2=22+(PM-1)2,
∴PM=
| 5 |
| 2 |
由勾股定理得:PN=
| PM2-MN2 |
| 3 |
| 2 |
∴PQ=3,∴②正确;
Q(-4,2),∴①正确;
△MPQ的面积是
| 1 |
| 2 |
OM=1+
| 3 |
| 2 |
| 5 |
| 2 |
故答案为:①②③.


练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目