题目内容

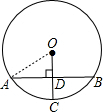
已知：如图，AB是⊙O的弦，OC⊥AB，垂足为D，⊙O的半径为5，CD=2，那么AB的长为______．
连接OA．
∵⊙O的半径为5，CD=2，
∵OD=5-2=3，即OD=3；
又∵AB是⊙O的弦，OC⊥AB，
∴AD=
1
2
AB；
在直角三角形ODC中，根据勾股定理，得
AD=
OA2-OD2
=4，
∴AB=8．
故答案是：8．
练习册系列答案
相关题目
如图，△ABC中，∠ACB=90°，AC=BC，CO为中线．现将一直角三角板的直角顶点放在点O上并绕点O旋转，若三角板的两直角边分别交AC，CB的延长线于点G，H．
（1）试写出图中除AC=BC，OA=OB=OC外其他所有相等的线段；
（2）请任选一组你写出的相等线段给予证明．
我选择证明______=______．
把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长为（　　）
A．3
2
B．5C．4D．
31
如图，半径为5的⊙P与y轴交于点M（0，-4），N（0，-10），函数y=
k
x
（x＜0）的图象过点P，则k=______．
已知：如图，AB是⊙O的直径，弦CD交AB于E点，BE=1，AE=5，∠AEC=30°，求CD的长．
如图，在平面直角坐标系中，⊙M与y轴相切于原点O，平行于x轴的直线交⊙M于P，Q两点，点P在点Q的右方，若点P的坐标是（-1，2），有下列结论：①点Q的坐标是（-4，2）；②PQ=3；③△MPQ的面积是3；④M点的坐标是（-3，0）．其中正确的结论序号是______．（多填或错填的得0分，少填的酌情给分）
如图，⊙O的直径AB垂直于弦CD，垂足是E，则下列结论错误的是（　　）
A．CE=DEB．
CB
=
BD
C．OE=BED．∠COE=∠DOE
已知：如图，在⊙O中，弦AB的长是半径OA的
3
倍，C为弧AB的中点．AB、OC相交于P点，求证：四边形OACB是菱形．
如图，已知AB为⊙O的直径，CD是弦，AB⊥CD于E，OF⊥AC于F，BE=OF．
（1）求证：△AFO≌△CEB；
（2）若EB=5cm，CD=10
3
cm，设OE=x，求x值及阴影部分的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网