题目内容
【题目】甲、乙两种型号的风扇成本分别为120元台、170元台,销售情况如下表所示(成本、售价均保持不变,利润=收入-成本):
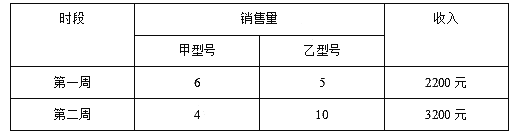
(1)求这两种型号风扇的售价;
(2)该商场打算再采购这两种型号的风扇共130台,销售完后总利润能不能恰好为8010元?若能,给出相应的采购方案;若不能,说明理由。
【答案】(1)甲型号风扇的售价为150元/台,乙型号风扇的售价为260元/台;(2)不能,理由见解析.
【解析】
(1)设甲型号风扇的售价为x元/台,乙型号风扇的售价为y元/台,根据总价=单价×数量结合表格中的数据,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购进甲型号风扇m台,则购进乙型号风扇(130-m)台,根据总利润=单台利润×销售数量,即可得出关于m的一元一次方程,解之即可得出m的值,由m的值不为整数,即可得出销售完后总利润不能恰好为8010元.
解:(1)设甲型号风扇的售价为x元/台,乙型号风扇的售价为y元/台,
根据题意得:![]()
解得:![]()
答:甲型号风扇的售价为150元/台,乙型号风扇的售价为260元/台.
(2)不能,理由如下:
设购进甲型号风扇m台,则购进乙型号风扇(130-m)台,
根据题意得:(150-120)m+(260-170)(130-m)=8010,
解得:m=![]()
∵![]() 不为整数,
不为整数,
∴销售完后总利润不能恰好为8010元.

【题目】在如图中,每个正方形由边长为1的小正方形组成: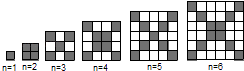
(1)观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 |
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1 , 白色小正方形的个数为P2 , 问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.