题目内容
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
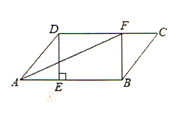
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
【答案】(1)详见解析;(2)20.
【解析】试题分析:(1)根据有一个角是90度的平行四边形是矩形可判定,
(2)首先证明AD=DF,求出AD即可解决问题.
试题解析: (1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,即BE∥DF,
∵CF=AE,
∴DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,∴∠DEB=90°,∴四边形BFDE是矩形.
(2)因为AB∥CD ,所以∠BAF=∠AFD,因为AF平分∠BAD,所以∠DAF=∠AFD,所以AD=DF,在直角三角形ADE中,因为AE=3,DE=4,所以AD=5,所以矩形的面积为20.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
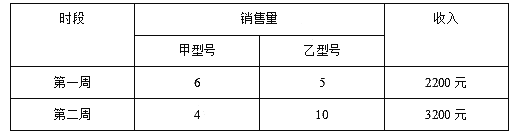
【题目】某校七年级(1)班体育委员统计了全班同学60秒跳绳次数,并列出了下面的不完整频数分布表和不完整的频数分布直方图.根据图表中的信息解答问题
组别 | 跳绳次数 | 频数 |
A | 60≤x<80 | 2 |
B | 80≤x<100 | 6 |
C | 100≤x<120 | 18 |
D | 120≤x<140 | 12 |
E | 140≤x<160 | a |
F | 160≤x<180 | 3 |
G | 180≤x<200 | 1 |
合计 | 50 | |
(1)求a的值;
(2)求跳绳次数x在120≤x<180范围内的学生的人数;
(3)补全频数分布直方图,并指出组距与组数分别是多少?