��Ŀ����
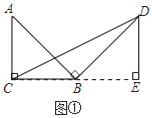
����Ŀ������ԭ�ͣ���ͼ�����ڵ���ֱ��������ABC�У���ACB=90����BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD������D����BCD��BC���ϵĸ�DE�� ��֤��ABC�ա�BDE���Ӷ��õ���BCD�����Ϊ![]() ��
��
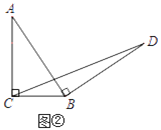
����̽������ͼ������Rt��ABC�У���ACB=90����BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD���ú�a�Ĵ���ʽ��ʾ��BCD���������˵�����ɣ�
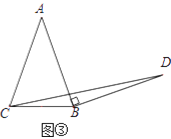
��Ӧ�ã���ͼ�����ڵ���������ABC�У�AB=AC��BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD��ֱ��д����BCD����������ú�a�Ĵ���ʽ��ʾ��
���𰸡�������
���������������:(1)����̽��:��ͼ��,����D��BC�Ĵ���,��BC���ӳ��߽��ڵ�E,�ɴ�ֱ�����ʾͿ��Եó���ABC�ա�BDE,����DE=BC=a,�����������ε������ʽ�ó�����,
(2)������:��ͼ��,����A��AF��BC��F,����D��DE��BC���ӳ����ڵ�E,�ɵ��������ε����ʿ��Եó�BF=![]() BC,���������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE,�������ε������ʽ�Ϳ��Եó�����.
BC,���������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE,�������ε������ʽ�Ϳ��Եó�����.
�������:(1)��BCD�����Ϊ![]() ,
,
����:��ͼ��,����D��BC�Ĵ���,��BC���ӳ��߽��ڵ�E,

���BED=��ACB=90��,
���߶�AB�Ƶ�B˳ʱ����ת90���õ��߶�BE,
��AB=BD,��ABD=90��,
���ABC+��DBE=90��,
�ߡ�A+��ABC=90��,
���A=��DBE,
�ڡ�ABC�͡�BDE��,
 ,
,
���ABC�ա�BDE��AAS��,
��BC=DE=a,
��S��BCD= ![]()
��S��BCD=![]() ,
,
(2)��Ӧ��:��ͼ��,����A��AF��BC��F,����D��DE��BC���ӳ����ڵ�E,
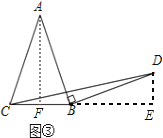
���AFB=��E=90��,BF= ![]() ,
,
���FAB+��ABF=90��,
�ߡ�ABD=90��,
���ABF+��DBE=90��,
���FAB=��EBD,
���߶�BD�����߶�AB��ת�õ���,
��AB=BD,
�ڡ�AFB�͡�BED��,
 ,
,
���AFB�ա�BED��AAS��,
��BF=DE= ![]() ,
,
��S��BCD= ![]() ,
,
��S��BCD=![]() ,
,
���BCD�����Ϊ![]() ,
,

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�����Ŀ�������ڿ����еĴ����ٶ�v(m/s)���¶�T(��)�Ĺ�ϵ���±���
�¶�/�� | 0 | 5 | 10 | 15 | 20 |
�ٶ�v/(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)д���ٶ�v���¶�T֮��Ĺ�ϵʽ��
(2)��T��30��ʱ���������Ĵ����ٶȣ�
(3)�������Ĵ����ٶ�Ϊ346m/sʱ���¶��Ƕ��٣�