äãá¢áÖàï
Àƒäãá¢À¢ÅÀû¼¡ªƒï£ˆòί̯ùáõ¥ÑüôýçäýáP37îÏü¯áÖàïȘÑå¤₤ò»y= ![]() x2çáë¥üµ¤ëÅåøò§½ÅÅêù䧃¢È˜ò姨àÓüôèÅý£ëõí«çá¿»°äý¿°ðëõí«ÈÛ
x2çáë¥üµ¤ëÅåøò§½ÅÅêù䧃¢È˜ò姨àÓüôèÅý£ëõí«çá¿»°äý¿°ðëõí«ÈÛ 
È´1ÈˋæåÝðê¢xçáàÀøçñÑöÏòúà¨äÍòçò»È˜xÆŠyçᥡæÕÑåÆÎò»øçàÓÝÚȤ
x | ÀÙ | ˋ4 | n | ˋ2 | ˋ1 | 0 | 1 | 2 | 3 | 4 | ÀÙ |
y | ÀÙ | 8 | 4.5 | 2 | 0.5 | 0 | 0.5 | 2 | 4.5 | 8 | ÀÙ |
óðøÅn=È£
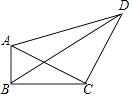
È´2ÈˋàÓë¥È˜åÖó§ûÌøݧú໧úÅöæ½ÝõüçxOyøÅȘØîûÒ°—êùØåèüÝÚøÅçáý¢ñøò»øçöˆæ½ÝõçáçÐȘ¡ªƒïûÒ°—çáçÐȘ£Ù°—¡û¤₤ò»çáǵøôë¥üµÈÛ
È´3Èˋ¡ªƒï£Ù°—çá¤₤ò»ë¥üµÈ˜ÅÀû¼¿ÜýšñÂüøȤ¡û¤₤ò»ÆÅæŸÅÀøçȘû£ÆÅæŸÇµøçÈ£çݤ₤ò»øçàÀæŸÅÀòÝȘæåÝðê¢xçáøçöˆ ÈÛ
È´4Èˋ§½Ø£ý§ä§ƒ¢¤₤ò»çáë¥üµñÂüøȤ Âìà¶çÐAÈ´xa Ș yaÈˋȘçÐBÈ´xb Ș ybÈˋåÖ¤₤ò»y= ![]() çáë¥üµèüÈ£
çáë¥üµèüÈ£
çÝxaÈ¥xbÈ¥0òÝȘyaÆŠybçáǵÅÀ¿ÄüçòúÈ£
çÝ0È¥xaÈ¥xbòÝȘyaÆŠybçáǵÅÀ¿ÄüçòúÈ£
ÂÖøÝüÔy1úÀ¤ûƒÙ¿»¤₤ò»çáë¥üµèüçáçÐÈ´ˋ2Ș2ÈˋÆŠÈ´1Ș0.5ÈˋÈ£çÝyÈ¥y1òÝȘxçáàÀøçñÑöÏòú ÈÛ
ÀƒÇÞ¯¡À¢
È´1Èˋ-3
È´2Èˋ§ãȤàÓë¥
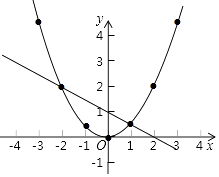
È´3Èˋ0
È´4ÈˋyaȃybÈ£ yaÈ¥ybÈ£ˋ2È¥xÈ¥1
Àƒ§ãö—À¢§ãȤȴ1ÈˋçÝy= ![]() x2=4.5òÝȘx=Àâ3Ș
x2=4.5òÝȘx=Àâ3Ș
ÀÁn=ˋ3ÈÛ
ùªØåÇÞ¯¡òúȤˋ3ÈÛ
ÂóûÒçÐÀÂê˜üÔȘ£Ù°—¤₤ò»ë¥üµÈÛ
Âú¿Üýš¤₤ò»ë¥üµ¢èøˆÈ¤éæöÿüÔçáÑËçÐæ½ÝõöˆÈ´0Ș0ÈˋȘ
ÀÁçÝx=0òÝȘyàÀæŸÅÀøçÈÛ
ùªØåÇÞ¯¡òúȤ0ÈÛ
ÂàÂì¿Üýš¤₤ò»ë¥üµ¢èøˆÈ¤çÝxÈ¥0òÝȘyøçùÌxøççáå—ǵѽ¥¾ÅÀÈ£çÝxȃ0òÝȘyøçùÌxøççáå—ǵѽå—ǵÈÛ
ÀÁçÝxaÈ¥xbÈ¥0òÝȘyaȃybÈ£çÝ0È¥xaÈ¥xbòÝȘyaÈ¥ybÈÛ
ùªØåÇÞ¯¡òúȤyaȃybÈ£yaÈ¥ybÈÛ
ÂÖåÖë¥øÅ£Ù°—øÝüÔy1Ș¿Üýš¤₤ò»ë¥üµ¢èøˆÈ¤çÝˋ2È¥xÈ¥1òÝȘøÝüÔåÖéæöÿüÔèüñ§È˜
ÀÁçÝyÈ¥y1òÝȘxçáàÀøçñÑöÏòúˋ2È¥xÈ¥1ÈÛ
ùªØåÇÞ¯¡òúȤˋ2È¥xÈ¥1ÈÛ
Àƒ¢¥çЃ¨ö—À¢â«ÆûѱÇö¤₤ò»çáë¥üµ¤ëѱÇö¤₤ò»çáÅåøòÑåäãᢧ½ÅÅéÅÑü¥Ç¢èçûç§ÇÞ¯¡È˜ÅÒ؈òšøˆÑ±Çö¤₤ò»ë¥üþ¿Ä¥■çÐȤ1À¢ˆ¢Öñ§ü·2ÀÂÑå°óøà 3ÀÂÑËçÐ 4ÀÂÆŠxøç£çÐ 5ÀÂÆŠyøç£çÐȣ嗥¾ÅåȤçÝa>0òÝȘÑå°óøÃæµÝÔȘyùÌxå—ǵѽ¥¾ÅÀÈ£Ñå°óøÃÆØÝÔȘyùÌxå—ǵѽå—ǵȣçÝa<0òÝȘÑå°óøÃæµÝÔȘyùÌxå—ǵѽå—ǵȣÑå°óøÃÆØÝÔȘyùÌxå—ǵѽ¥¾ÅÀÈÛ

 øú£Ü¢öäûûɃÚ100ñøçË刿»¿Ä¥šýãüçêÅÇÞ¯¡
øú£Ü¢öäûûɃÚ100ñøçË刿»¿Ä¥šýãüçêÅÇÞ¯¡ çËåˆóÖøÅóÖáˋƒÚüçêÅÇÞ¯¡
çËåˆóÖøÅóÖáˋƒÚüçêÅÇÞ¯¡Àƒäãá¢À¢á°§£ƒ₤åÖØ£¡—ôñ¢Öë°¥óçáá°òÝÑöâÇ몰çêƒçá°çùìúÕ¢—àÓÝÚȤ
°çùìÈ´km/hÈˋ | 48 | 49 | 50 | 51 | 52 |
°çêƒò»È´êƒÈˋ | 5 | 4 | 8 | 2 | 1 |
å·èüò—°çùìçáøÅö£ò»¤ëøÖò»ñøÝÞòúÈ´ Èˋ
A.50Ș8
B.50Ș50
C.49Ș50
D.49Ș8