题目内容
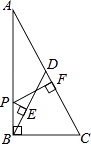
【题目】如图所示，一个角60°的三角形纸片，剪去这个60°角后，得到一个四边形，则∠1+∠2= ． 
【答案】240°
【解析】解：根据三角形的内角和定理得：
四边形除去∠1，∠2后的两角的度数为180°﹣60°=120°，
则根据四边形的内角和定理得：
∠1+∠2=360°﹣120°=240°．
所以答案是：240°．
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识，掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角，以及对多边形内角与外角的理解，了解多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°．
【题目】小明根据华师版八年级下册教材P37学习内容，对函数y= 
x2的图象和性质进行了探究，试将如下尚不完整的过程补充完整． 
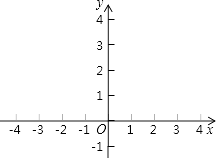
（1）自变量x的取值范围是全体实数，x与y的几组对应数值如表：
x | … | ﹣4 | n | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 8 | 4.5 | 2 | 0.5 | 0 | 0.5 | 2 | 4.5 | 8 | … |
其中n=；
（2）如图，在平面直角三角形坐标系xOy中，已描出了以上表中的部分数值为坐标的点，根据描出的点，画出该函数的大致图象．
（3）根据画出的函数图象，小明观察发现：该函数有最小值，没有最大值；当函数值取最小时，自变量x的值为 ．
（4）进一步探究函数的图象发现： ①若点A（xa ， ya），点B（xb ， yb）在函数y= 
的图象上；
当xa＜xb＜0时，ya与yb的大小关系是；
当0＜xa＜xb时，ya与yb的大小关系是；
②直线y1恰好经过函数的图象上的点（﹣2，2）与（1，0.5）；当y＜y1时，x的取值范围是 ．
