题目内容
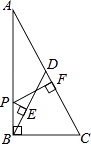
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5 ![]() ,则BD的长为 .
,则BD的长为 . 
【答案】![]()
【解析】解:作DM⊥BC,交BC延长线于M,如图所示:
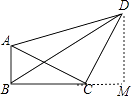
则∠M=90°,
∴∠DCM+∠CDM=90°,
∵∠ABC=90°,AB=3,BC=4,
∴AC2=AB2+BC2=25,
∴AC=5,
∵AD=5 ![]() ,CD=5,
,CD=5,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠CDM,
∵∠ABC=∠M=90°,
∴△ABC∽△CMD,
∴ ![]() =
= ![]() =
= ![]() =1,
=1,
∴CM=AB=3,DM=BC=4,
∴BM=BC+CM=7,
∴BD= ![]() =
= ![]() =
= ![]() ,
,
故答案为: ![]() .
.
作DM⊥BC,交BC延长线于M,由勾股定理得出AC2=AB2+BC2=25,求出AC2+CD2=AD2,由勾股定理的逆定理得出△ACD是直角三角形,∠ACD=90°,证出∠ACB=∠CDM,得出△ABC∽△CMD,由相似三角形的对应边成比例求出CM=AB=3,DM=BC=4,得出BM=BC+CM=7,再由勾股定理求出BD即可

【题目】小明根据华师版八年级下册教材P37学习内容,对函数y= ![]() x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整.
x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整. 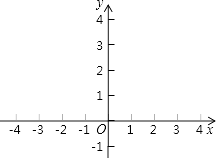
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
x | … | ﹣4 | n | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 8 | 4.5 | 2 | 0.5 | 0 | 0.5 | 2 | 4.5 | 8 | … |
其中n=;
(2)如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.
(3)根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为 .
(4)进一步探究函数的图象发现: ①若点A(xa , ya),点B(xb , yb)在函数y= ![]() 的图象上;
的图象上;
当xa<xb<0时,ya与yb的大小关系是;
当0<xa<xb时,ya与yb的大小关系是;
②直线y1恰好经过函数的图象上的点(﹣2,2)与(1,0.5);当y<y1时,x的取值范围是 .