题目内容
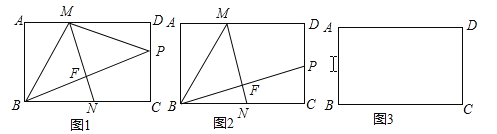
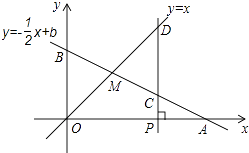
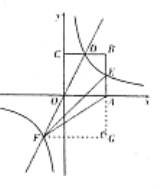
【题目】如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，其边长为2，点A，点C分别在
轴，
轴的正半轴上．函数
的图象与CB交于点D，函数
（
为常数，
）的图象经过点D，与AB交于点E，与函数的图象在第三象限内交于点F，连接AF、EF．
（1）求函数的表达式，并直接写出E、F两点的坐标．
（2）求△AEF的面积．
【答案】（1）
，E（2，1），f（-1，-2）；（2）
．
【解析】
试题分析：（1）先得到点D的坐标，再求出k的值即可确定反比例函数解析式；
（2）过点F作FG⊥AB，与BA的延长线交于点G．由E、F两点的坐标，得到AE=1，FG=2-（-1）=3，从而得到△AEF的面积．
试题解析：（1）∵正方形OABC的边长为2，∴点D的纵坐标为2，即y=2，将y=2代入y=2x，得到x=1，∴点D的坐标为（1，2）．∵函数
的图象经过点D，∴
，∴k=2，∴函数的表达式为
．
（2）过点F作FG⊥AB，与BA的延长线交于点G．∵E、F两点的坐标分别为（2，1），（-1，-2），∴AE=1，FG=2-（-1）=3，∴△AEF的面积为：
AEFG=
=
.
【题目】小明根据华师版八年级下册教材P37学习内容，对函数y= 
x2的图象和性质进行了探究，试将如下尚不完整的过程补充完整．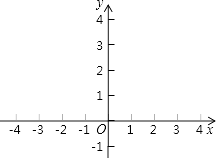 
（1）自变量x的取值范围是全体实数，x与y的几组对应数值如表：
x | … | ﹣4 | n | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 8 | 4.5 | 2 | 0.5 | 0 | 0.5 | 2 | 4.5 | 8 | … |
其中n=；
（2）如图，在平面直角三角形坐标系xOy中，已描出了以上表中的部分数值为坐标的点，根据描出的点，画出该函数的大致图象．
（3）根据画出的函数图象，小明观察发现：该函数有最小值，没有最大值；当函数值取最小时，自变量x的值为 ．
（4）进一步探究函数的图象发现： ①若点A（xa ， ya），点B（xb ， yb）在函数y= 
的图象上；
当xa＜xb＜0时，ya与yb的大小关系是；
当0＜xa＜xb时，ya与yb的大小关系是；
②直线y1恰好经过函数的图象上的点（﹣2，2）与（1，0.5）；当y＜y1时，x的取值范围是 ．
