��Ŀ����
����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���y��![]() +x��ͼ�������ʽ�����̽����̽���������£��벹��������
+x��ͼ�������ʽ�����̽����̽���������£��벹��������
(1)����y��![]() +x���Ա���x��ȡֵ��Χ���� ����
+x���Ա���x��ȡֵ��Χ���� ����
(2)�±���y��x�ļ����Ӧֵ��
x | �� | ��3 | ��2 | ��1 | 0 |
|
|
|
| 2 | 3 | 4 | 5 | �� |
y | �� | �� | �� | �� | ��1 | �� | �� |
|
| 3 |
| m |
| �� |
��m��ֵ��
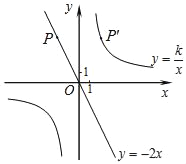
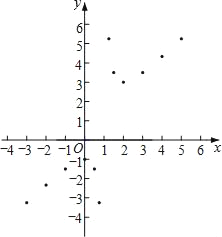
(3)��ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��
(4)��һ��̽�����֣��ú���ͼ���ڵ�һ�����ڵ���͵��������(2��3)����Ϻ�����ͼ��д���ú�������������(һ������)���� ����
(5)С�����֣����ú�����ͼ����ڵ�(�� ������ ��)�����ĶԳƣ�
���ú�����ͼ����һ����ֱ��x���ֱ�����㣬������ֱ��Ϊ�� ����
��ֱ��y��m��ú�����ͼ�����㣬��m��ȡֵ��ΧΪ�� ����
���𰸡�(1)x��1,(2)![]() ,(4)x��2ʱy��x�����������,
,(4)x��2ʱy��x�����������,
(5)��( ![]() ��
��![]() )����x=1������1��m��3.
)����x=1������1��m��3.
��������
��1�����ĸ�������㼴���������x��ȡֵ��Χ��
��2����x=4����y=![]() +x�������m��ֵ��
+x�������m��ֵ��
��3���ù⻬���߰Ѹ���˳�����Ӽ��ɣ�
��4������ͼ���ɣ���x��2ʱy��x������������𰸲�Ψһ����
��5������ͼ����.
��1������y=![]() +x���Ա���x��ȡֵ��Χ��x��1��
+x���Ա���x��ȡֵ��Χ��x��1��
�ʴ�Ϊx��1��
��2��x=4ʱ��y=![]() ��
��
��m=![]() ��
��
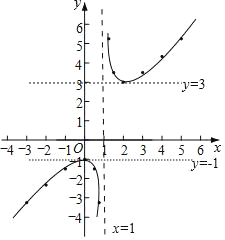
��3������ͼ����ͼ��ʾ��
��4��x��2ʱy��x������������𰸲�Ψһ��
�ʴ�Ϊ��x��2ʱy��x�����������
��5���ٸú�����ͼ����ڵ㣨1��1�������ĶԳƣ�
�ڸú�����ͼ����һ����ֱ��x���ֱ�����㣬������ֱ��Ϊx=1��
��ֱ��y=m��ú�����ͼ�����㣬��m��ȡֵ��ΧΪ��1��m��3��
�ʴ�Ϊ1��1��x=1����1��m��3��

 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�����Ŀ��Ϊ�˲μ�����������Сѧ����ʫ�ʴ������ijУ���꼶������ѧ��������Ԥѡ�����а���ǰ5��ѧ���ijɼ����ٷ��ƣ��ֱ�Ϊ���ˣ�1����86��85��77��92��85���ˣ�2����79��85��92��85��89��ͨ�����ݷ������б����£�
�༶ | ƽ���� | ��λ�� | ���� | ���� |
�ˣ�1�� | 85 | b | c | 22.8 |
�ˣ�2�� | a | 85 | 85 | 19.2 |
��1��ֱ��д������a��b��c��ֵ��
��2�������������ݷ���������Ϊ�ĸ���ǰ5��ͬѧ�ijɼ��Ϻã�˵�����ɣ�