��Ŀ����
����Ŀ��Ϊ�˽�ij��ѧѧ�����������ڼ��Լ�����������˷��������IJ��������Сǿ��ȫУ��Χ�������ȡ��������ѧ������ij���緹�˷ѷ�����������˵��飬���������ݷ�Ϊ���飺![]() ���Ͳ�ȫ�����ꣻ
���Ͳ�ȫ�����ꣻ![]() ����ʣ�����˳��ꣻ
����ʣ�����˳��ꣻ![]() �������굫����ʣ��
�������굫����ʣ��![]() �����Ͳ˶���ʣ.���ݵ���������������ͼ��ʾ������������ͳ��ͼ.
�����Ͳ˶���ʣ.���ݵ���������������ͼ��ʾ������������ͳ��ͼ.

�ش��������⣺
��1����α�����ѧ������ �ˣ�����ͳ��ͼ�У���![]() ��������Ӧ��Բ�ĽǵĶ���Ϊ ��
��������Ӧ��Բ�ĽǵĶ���Ϊ ��
��2����ȫ����ͳ��ͼ��
��3����֪����ѧ����ѧ��![]() �ˣ�����������緹��ʣ����ѧ������������ƽ��ÿ��ʣ
�ˣ�����������緹��ʣ����ѧ������������ƽ��ÿ��ʣ![]() �������㣬�����緹���˷Ѷ���ǧ������
�������㣬�����緹���˷Ѷ���ǧ������
���𰸡���1��120��72������2������������3��������ʣ����ѧ������Ϊ��750�ˣ������緹���˷�7.5ǧ����.
��������
��1����A����������A��ռ�İٷֱȼ��ɵõ�������ѧ�����������������B��ռ�������İٷֱ��ٳ���360���������B������Ӧ��Բ�ĽǵĶ�����
��2���ȸ������������C������������ɲ�ȫ����ͼ��
��3�������2500������ʣ����ѧ����������������������10���ɵó�ʣ���Ŀ���������ٽ��е�λת�����ɵó���.
�⣺��1����α�����ѧ������Ϊ��72��60%=120���ˣ�
��B��������Ӧ��Բ�ĽǵĶ�����24��120��360��=72��
��2��C�������Ϊ��120��10%=12���ˣ�
����ͳ��ͼ���£�
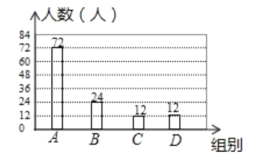
��3����ʣ����ѧ������Ϊ��2500����1-60%-10%��=750���ˣ�
750��10=7500���ˣ�=7.5��ǧ�ˣ�
�������緹���˷�7.5ǧ����.

 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���y��![]() +x��ͼ�������ʽ�����̽����̽���������£��벹��������
+x��ͼ�������ʽ�����̽����̽���������£��벹��������
(1)����y��![]() +x���Ա���x��ȡֵ��Χ���� ����
+x���Ա���x��ȡֵ��Χ���� ����
(2)�±���y��x�ļ����Ӧֵ��
x | �� | ��3 | ��2 | ��1 | 0 |
|
|
|
| 2 | 3 | 4 | 5 | �� |
y | �� | �� | �� | �� | ��1 | �� | �� |
|
| 3 |
| m |
| �� |
��m��ֵ��
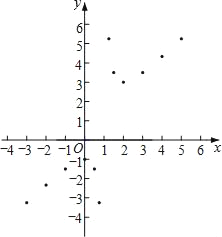
(3)��ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��
(4)��һ��̽�����֣��ú���ͼ���ڵ�һ�����ڵ���͵��������(2��3)����Ϻ�����ͼ��д���ú�������������(һ������)���� ����
(5)С�����֣����ú�����ͼ����ڵ�(�� ������ ��)�����ĶԳƣ�
���ú�����ͼ����һ����ֱ��x���ֱ�����㣬������ֱ��Ϊ�� ����
��ֱ��y��m��ú�����ͼ�����㣬��m��ȡֵ��ΧΪ�� ����