题目内容
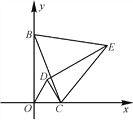
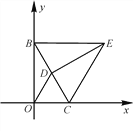
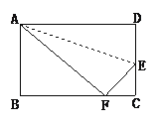
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,在
,在![]() 上截取
上截取![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,则
,则![]() ____________.
____________.
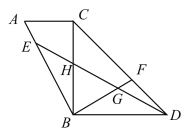
【答案】![]()
【解析】
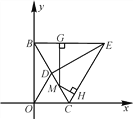
过点D作DM⊥BD,与BF延长线交于点M,先证明△BHE≌△BGD得到∠EHB=∠DGB,再由平行和对顶角相等得到∠MDG=∠MGD,即MD=MG,在△△BDM中利用勾股定理算出MG的长度,得到BM,再证明△ABC≌△MBD,从而得出BM=AB即可.
解:∵AC∥BD,∠ACB=90°,
∴∠CBD=90°,即∠1+∠2=90°,
又∵BF⊥AB,
∴∠ABF=90°,
即∠8+∠2=90°,
∵BE=BD,
∴∠8=∠1,
在△BHE和△BGD中,
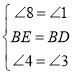 ,
,
∴△BHE≌△BGD(ASA),
∴∠EHB=∠DGB
∴∠5=∠6,∠6=∠7,
∵MD⊥BD
∴∠BDM=90°,
∴BC∥MD,
∴∠5=∠MDG,
∴∠7=∠MDG
∴MG=MD,
∵BC=7,BG=4,
设MG=x,在△BDM中,
BD2+MD2=BM2,
即![]() ,
,
解得x=![]() ,
,
在△ABC和△MBD中
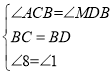 ,
,
∴△ABC≌△MBD(ASA)
AB=BM=BG+MG=4+![]() =
=![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案【题目】某班“数学兴趣小组”对函数y=![]() +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.
(1)函数y=![]() +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 |
|
|
|
| 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | ﹣1 | ﹣ | ﹣ |
|
| 3 |
| m |
| … |
求m的值;
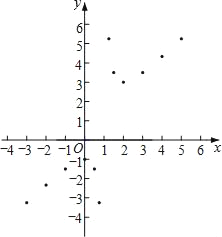
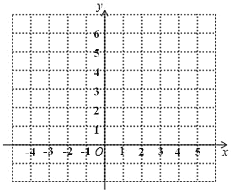
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可): .
(5)小明发现,①该函数的图象关于点( , )成中心对称;
②该函数的图象与一条垂直于x轴的直线无交点,则这条直线为 ;
③直线y=m与该函数的图象无交点,则m的取值范围为 .