��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���C�İ뾶Ϊr��P����Բ��C���غϵĵ㣬��P������C�ķ��Ƶ�Ķ������£���������CP�ϴ���һ��P�䣬����CP+CP��=2r�����P��Ϊ��P������C�ķ��Ƶ㣬��ͼΪ��P���������C�ķ��Ƶ�P���ʾ��ͼ��
�ر�أ�����P����Բ��C�غ�ʱ���涨CP��=0��
��1������O�İ뾶Ϊ1ʱ��
���ֱ��жϵ�M��2��1����N��![]() ��0����T��1��
��0����T��1�� ![]() ��������O�ķ��Ƶ��Ƿ���ڣ������ڣ��������ꣻ
��������O�ķ��Ƶ��Ƿ���ڣ������ڣ��������ꣻ
����P��ֱ��y=��x+2�ϣ�����P������O�ķ��Ƶ�P����ڣ��ҵ�P�䲻��x���ϣ����P�ĺ������ȡֵ��Χ��
��2����C��Բ����x���ϣ��뾶Ϊ1��ֱ��y=��![]() x+2
x+2![]() ��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P������C�ķ��Ƶ�P������C���ڲ�����Բ��C�ĺ������ȡֵ��Χ��
��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P������C�ķ��Ƶ�P������C���ڲ�����Բ��C�ĺ������ȡֵ��Χ��

���𰸡���1��������������0��x��2����2��Բ��C�ĺ������ȡֵ��Χ��2��x��8��
�������������������1�� �����ݷ��Ƶ�Ķ��廭ͼ�ó����ۣ��ڡ�CP��2r��2 CP2��4�� P��x����x��2���� CP2��x2������x��2��2��2x2��4x��4����2x2��4x��0�� x��x��2����0����0��x��2����x��2��x=0������֤���ɵó���P��2��0����P����2��0������������P��0��2����P����0��0�����������⣬��0��x��2
��2�����A��B�����꣬�ó�OA��OB�ı�ֵ���Ӷ������OAB=30������C��x��0��
����C��OA��ʱ����CH��AB��H����CH��CP��2r��2����AC��4���ó� C�������x��2�� ����x��2ʱ��C�����꣨2��0����H��ķ��Ƶ�H����2��0����Բ���ڲ���������C��A���Ҳ�ʱ��C���߶�AB�ľ���ΪAC����AC���ֵΪ2����C�������x��8���ó�����.
��������� ��1���⣺��M��2��1�������ڣ� ![]() ���ڣ����Ƶ�
���ڣ����Ƶ�![]()
![]() ���ڣ����Ƶ�T����0��0��
���ڣ����Ƶ�T����0��0��
�ڡ�CP��2r��2 CP2��4�� P��x����x��2���� CP2��x2������x��2��2��2x2��4x��4��4
2x2��4x��0�� x��x��2����0����0��x��2����x��2ʱ��P��2��0����P����2��0������������
��x��0ʱ��P��0��2����P����0��0�����������⣬��0��x��2
��2���⣺������ã�A��6��0����![]() ����
����![]() �����OAB��30������C��x��0��
�����OAB��30������C��x��0��
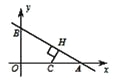
����C��OA��ʱ����CH��AB��H����CH��CP��2r��2����AC��4�� C�������x��2��
����x��2ʱ��C�����꣨2��0����H��ķ��Ƶ�H����2��0����Բ���ڲ���
����C��A���Ҳ�ʱ��C���߶�AB�ľ���ΪAC����AC���ֵΪ2����C�������x��8
����������Բ��C�ĺ������ȡֵ��Χ2��x��8��