题目内容
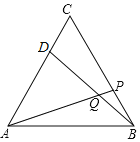
【题目】如图,在△ABC中,∠ACB=![]() ,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
(1)求证:四边形ECBF是平行四边形;
(2) 当∠A=![]() 时,求证:四边形ECBF是菱形.
时,求证:四边形ECBF是菱形.

【答案】(1)详见解析;(2)详见解析.
【解析】
试题(1)根据三角形的中位线定理可得EF∥BC,根据两组对边分别平行的四边形是平行四边形即可判定四边形ECBF是平行四边形;(2)根据直角三角形中30°的锐角所对的直角边等于斜边的一半和斜边的中线等于斜边的一半可得![]() ,
,![]() ,即可得
,即可得![]() ,根据一组邻边相等的平行四边形是菱形即可判定四边形ECBF是菱形.
,根据一组邻边相等的平行四边形是菱形即可判定四边形ECBF是菱形.
试题解析: (1) 证明:∵D,E分别为边AC,AB的中点,
∴DE∥BC,即EF∥BC.
又∵BF∥CE,
∴四边形ECBF是平行四边形.
(2)证法一:
∵∠ACB=![]() ,∠A=
,∠A=![]() ,E为AB的中点,
,E为AB的中点,
∴![]() ,
,![]() .
.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
证法二:
∵∠ACB=![]() ,∠A=
,∠A=![]() ,E为AB的中点,
,E为AB的中点,
∴![]() ,∠ABC=
,∠ABC=![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.
证法三:
∵E为AB的中点,∠ACB=![]() ,∠A=
,∠A=![]() ,
,
∴![]() , ∠ABC=
, ∠ABC=![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
又由(1)知,四边形ECBF是平行四边形,
∴四边形ECBF是菱形.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目