题目内容
【题目】如图,在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发,分别都以每分钟1个单位的速度由C向A和由B向C爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、P处,请问:
(1)在爬行过程中,BD和AP始终相等吗?
(2)在爬行过程中BD与AP所成的∠DQA有变化吗?若无变化是多少度?
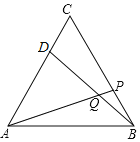
【答案】(1)BD和AP始终相等;(2)∠DQA大小无变化,始终是60°.
【解析】
(1)根据等边三角形性质得出∠CAB=∠C=∠ABP=60°,AB=BC,根据SAS推出△BDC≌△APB即可.
(2)根据△BDC≌△APB得出∠CBD=∠BAP,根据三角形外角性质求出∠DQA=∠ABC,即可求出答案.
解:(1)在爬行过程中,BD和AP始终相等,
理由是:∵△ABC是等边三角形,
∴∠CAB=∠C=∠ABP=60°,AB=BC,
在△BDC和△APB中,
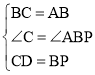 ,
,
∴△BDC≌△APB(SAS),
∴BD=AP.
(2)蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,
理由:∵△BDC≌△APB,
∴∠CBD=∠BAP,
∴∠DQA=∠DBA+∠BAP=∠DBA+∠CBD=∠ABC=60°,
即蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,始终是60°.

练习册系列答案
相关题目






