题目内容
【题目】如图,将矩形![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿
沿![]() 折叠压平,使点
折叠压平,使点![]() 落在坐标平面内,设点
落在坐标平面内,设点![]() 的对应点为点
的对应点为点![]() .若抛物线
.若抛物线![]() (
(![]() 且
且![]() 为常数)的顶点落在
为常数)的顶点落在![]() 的内部,则
的内部,则![]() 的取值范围是( )
的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
利用对折的性质,得到线段的关系,用勾股定理建立方程,最后用相似△AFG∽△ABD得到比例式![]() ,计算出点G,H的纵坐标即可.
,计算出点G,H的纵坐标即可.
如图,
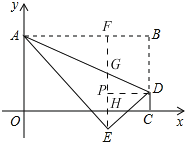
过点E作EF⊥AB于F,EF分别与AD、OC交于点G、H,
过点D作DP⊥EF于点P,
则EP=PH+EH=DC+EH=1+EH,
在Rt△PDE中,由勾股定理可得,
DP2=DE2-PE2=9+(1+EH)2,
∴BF2=DP2=9+(1+EH)2,
在Rt△AEF中,AF=AB-BF=3![]() -
-![]() ,EF=4+EH,AE=4,
,EF=4+EH,AE=4,
∵AF2+EF2=AE2,
即:(3![]() -
-![]() )2+(4+EH)2=16,
)2+(4+EH)2=16,
解得EH=1,
∴AB=3![]() ,AF=2
,AF=2![]() ,E(2
,E(2![]() ,-1).
,-1).
∵∠AFG=∠ABD=90°,∠FAG=∠BAD,
∴△AFG∽△ABD.
∴![]() ,
,
即:![]() ,
,
∴FG=2.
∴EG=EF-FG=3.
∴点G的纵坐标为2.
∵y=ax2-4![]() ax+10=a(x-2
ax+10=a(x-2![]() )2+(10-20a),
)2+(10-20a),
∴此抛物线y=ax2-4![]() ax+10的顶点必在直线x=2
ax+10的顶点必在直线x=2![]() 上.
上.
又∵抛物线的顶点落在△ADE的内部,
∴此抛物线的顶点必在EG上.
∴-1<10-20a<2,
∴![]() .
.
故选B.

练习册系列答案
相关题目