题目内容
【题目】A、B两地相距40km,甲、乙两人沿同一路线从A地到B地,甲骑自行车先出发,1.5h后乙乘坐公共汽车出发,两人匀速行驶的路程与时间的关系如图所示.
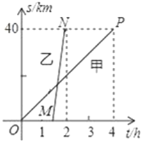
(1)求甲、乙两人的速度;
(2)若乙到达B地后,立即以原速返回A地.
①在图中画出乙返程中距离A地的路程y(km)与时间x(h)的函数图象,并求出此时y与x的函数表达式;
②求甲在离B地多远处与返程中的乙相遇?
【答案】(1)甲、乙两人的速度分别是10km/h,80km/h;(2)①函数图象见解析;y=80x+200;②甲在离B地![]() km处与返程中的乙相遇.
km处与返程中的乙相遇.
【解析】
(1)根据函数图象,利用速度=路程÷时间进行计算;
(2)①根据乙是原速返回A地,可知同样是0.5小时行驶了40km,然后可画出函数图象,判断出点(2,40),(2.5,0)在此函数的图象上,进而利用待定系数法求解析式即可;②先求出甲的函数解析式,然后可以求得甲乙相遇时的时间以及距A地的距离,从而可以求得甲在离B地多远处与返程中的乙相遇.
解:(1)由图可知:
甲4小时行驶了40km,则甲的速度为:40÷4=10km/h,
乙0.5小时行驶了40km,则乙的速度为:40÷0.5=80km/h,
即甲、乙两人的速度分别是10km/h,80km/h;
(2)①乙返程中距离A地的路程y(km)与时间x(h)的函数图象如图所示:
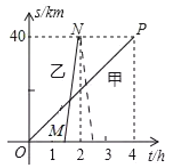
设乙返程中距离A地的路程y(km)与时间x(h)的函数解析式是y=kx+b(k≠0),
∵点(2,40),(2.5,0)在此函数的图象上,
∴![]() ,解得
,解得![]() ,
,
即乙返程中距离A地的路程y(km)与时间x(h)的函数表达式为:y=80x+200;
②设甲行驶过程对应的函数解析式是:y=mx(m≠0),
代入(4,40)得40=4m,解得m=10,
∴甲行驶过程对应的函数解析式是:y=10x,
联立![]() ,解得
,解得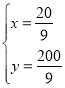 ,
,
∵![]() ,
,
∴甲在离B地![]() km处与返程中的乙相遇.
km处与返程中的乙相遇.