Question

【题目】如图，PA切⊙于点A，OP交⊙O于点B，且点B为OP的中点，弦AC∥OP．若OP=2，则图中阴影部分的面积为（ ）

A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：连结OA、OC，如图，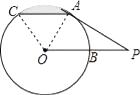

∵PA切⊙于点A，∴OA⊥PA，∴∠OAP=90°，
∵点B为OP的中点，∴OB=PB，∴OA= OP=1，
∴∠P=30°，∠POA=60°，
∵AC∥OP，∴∠OAC=∠POA=60°，
而OA=OC，∴△OAC为等边三角形，∴∠AOC=60°，
∴图中阴影部分的面积=S扇形AOC﹣S△AOC= ．
故选C．
【考点精析】关于本题考查的扇形面积计算公式，需要了解在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）才能得出正确答案．