Question

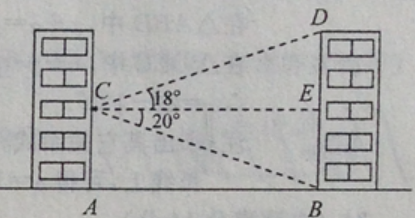
【题目】如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB=30m.
（结果精确到0.1m。参考数据：tan20°≈0.36,tan18°≈0.32）

（1）求∠BCD的度数.
（2）求教学楼的高BD

Answer 1

【答案】
（1）

解：过点C作CD⊥BD于点E，

则∠DCE=18°，∠BCE=20°，

所以∠BCD=∠DCE+∠BCE=18°+20°=38°.

（2）

解：由已知得CE=AB=30（m）,

在Rt△CBE中，BE=CE×tan20°≈30×0.36=10.80(m)，

在Rt△CDE中，DE=CE×tan18°≈30×0.32=9.60(m)，

∴教学楼的高BD=BE+DE=10.80+9.60≈20.4（m）.

答：教学楼的高为20.4m.

【解析】（1）C观测D的仰角应为CD与水平面的较小的夹角，即∠DCE；C观测B的俯角应为CB与水平线的较小的夹角，即为∠BCE，不难得出∠BCD=∠DCE+∠BCE；（2）易得CE=AB，则由直角三角形的锐角函数值即可分别求得BE和DE，求和即可.
【考点精析】利用关于仰角俯角问题对题目进行判断即可得到答案，需要熟知仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．