题目内容
【题目】如图，在平面直角坐标系xOy中，已知点A（﹣1，0），B（﹣1，1），C（1，0），D（1，2），点P是坐标系内一点，给出定义：若存在过点P的直线l与线段AB，CD都有公共点，则称点P是线段AB，CD的“联络点”．现有点P（x，y）在直线y= 
x上，且它是线段AB，CD的“联络点”，则x的取值范围是 ． 
【答案】x≤﹣ 
或x≥0
【解析】解：作直线BD、BC、AD以及y= 
x，如图所示．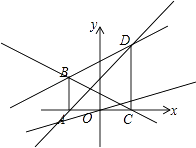
设直线AD的解析式为y=kx+b，
将点A（﹣1，0）、D（1，2）代入y=kx+b中，
得： 
，解得： 
，
∴直线AD的解析式为y=x+1．
观察图形可知：
当x≥0时，直线y= x在x轴（包括x轴上）于直线AD之间，此时直线y= x上的点均为“联络点”；
当x＜0时，联立直线y= x与直线AD成方程组，
得： 
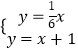，解得：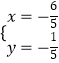 
，
直线y= 在x≤﹣ 中时，图象在直线AD（包括直线AD上的点）、BC之间，
∴当x≤﹣ 时，直线y= x上的点均为“联络点”．
故x的取值范围为：x≤﹣ 或x≥0．
所以答案是：x≤﹣ 或x≥0．
【考点精析】解答此题的关键在于理解一次函数的图象和性质的相关知识，掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远．
练习册系列答案
相关题目
